Wyznacz dziedzinę
Dżonyyy: | | x + 1 | | √3−x | |
f(x)= |
| + |
| |
| | √x + 4 | | (x−1)(x−5) | |
(x−1)(x−5)≠0
x−1≠0 V x−5≠0
x≠1 V x≠5
D=R\{1;5}
√x + 4≠0
I dalej nie wiem jak to zrobić
2 gru 11:42
Jerzy:
Po pierwsze: x ≠ −1 i x ≠ 5
Po drugie: x ≥ 0
Po trzecie: 3 − x ≥ 0
Po czwarte: √x + 4 ≠ 0
2 gru 11:45
Jerzy:
1) oczywiście : x ≠ 1 i x ≠ 5
2 gru 11:46
Jacob: √x≠−4 czyli z tego nie wyrzucasz nic z dziedziny ale sam x>=0
trzeci warunek 3−x>=0
2 gru 11:48
Jacob: liczysz wszystkie warunki i łaczysz je w całość
2 gru 11:49
Dżonyyy: Dlaczego 3 − x ≥ 0
przecież to jest w liczniku
Czyli że zamiast √x + 4 ≠ 0 można zapisać po prostu x≥0
2 gru 12:08
Jerzy:
Liczba pod pierwiastkiem musi być nieujemmna.
√x + 4 ≠ 0 dla każdego x ≥ 0
2 gru 12:09
Dżonyyy: Dobrze. A dlaczego 3 warunkiem jest 3 − x ≥ 0
2 gru 12:12
Dżonyyy: I jak zapisać dziedzinę do warunku x≥0
2 gru 12:13
Jerzy:
Już napisałem..... 3 − x ≥ 0 , bo to liczba pod pierwiastkiem.
2 gru 12:14
Dżonyyy: Yhm. Czyli że jakbym miał przykład:
To :
x≥0
i potem:
4 − x ≥ 0 , tak
2 gru 12:17
2 gru 12:17
Jerzy:
Nie..
1) x2 − 3 ≠ 0
2) 4 − x ≥ 0
2 gru 12:18
Jerzy:
to dokładasz: x > 0
2 gru 12:18
Dżonyyy: x > 0 odwołuje się do
√x tak
2 gru 12:21
Jerzy:
Tak.
2 gru 12:22
Dżonyyy: To mam tak:
1) x>0
2)
x
2−3≠0
x
2≠3
x≠
√3 lub x≠−
√3
3)
x≥0
4−x≥0
−x≥−4
x≤4
No tak, tylko jak do tego wszystkiego dziedzinę wyznaczyć
2 gru 12:25
Jerzy:
Najlepiej na osi liczbowej, tak jak Ci pokazałem w innym zadaniu.
2 gru 12:27
Jerzy:
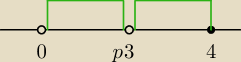
2 gru 12:30
Dżonyyy: Aa jak mam do tego jeszcze:
2 gru 12:41
Dżonyyy: | | 3x − 2 | | √4−x | | 1 | |
* |
| + |
| − |
| |
| | lxl − 1 | | x2 − 3 | | √x | |
2 gru 12:43
Jerzy:
Dokładasz: |x| ≠ 1 ⇔ x ≠ 1 i x ≠ −1
2 gru 12:46
Dżonyyy:
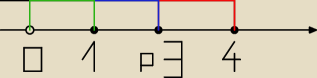
To teraz tak będzie?
2 gru 12:56
Jerzy:
Z rysunku 12:30 'wyciągasz" x = 1
2 gru 13:08
Dżonyyy: To jak to będzie?
2 gru 13:18
Jerzy:
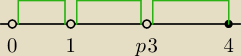
2 gru 13:21
Dżonyyy: Aha czyli tak po kolei trzeba lecieć
A dziedzina z tego jaka wyjdzie?
(0;4>
2 gru 13:35
Jerzy:
Suma tych przedziałów.
2 gru 13:36
Dżonyyy: (0;1) U (1;
√3) U (
√3;4>
Dobrze teraz jest
2 gru 13:38
Jerzy:
Tak.
2 gru 13:38
Dżonyyy: Dzięki wielkie
Zostało mi jeszcze coś takiego:
1) f(x) = ln(x
2 − 4x + 3)
2) f(x) = log
2(4 −
√x)
Nie mam pojęcia od czego tutaj zacząć
2 gru 13:41
Jerzy:
1) x2 − 4x + 3 > 0
2) x ≥ 0 i 4 − √x > 0
2 gru 13:43
Dżonyyy: w 1) x1 = 1 ; x2 = 3
i dziedzina wyszła D=xE(−
∞;1) U (3;+
∞) , tak
2 gru 14:01
Dżonyyy: A w 2 przykadzie:
x ≥ 0 i 4 −
√x>0
√x<4/* pierwiastek
x<2
I D=xE<0;2>
2 gru 14:03