monotonicznosc i ekstrema
kasia: monotonicznosc funkcji i ekstrema
2 gru 08:18
kasia: drugi przyklad:
y= |x2+2x−3|
2 gru 08:20
Jerzy:
Potrafisz określić dziedzinę i policzyć pochodną ?
2 gru 08:22
kasia: w pierwszym przykładzie tak, gorzej z miejscami zerowymi
w drugim − nie
2 gru 08:23
Jerzy:
OK. Kiedy zeruje się pochodna w pierwszym przykładzie ?
2 gru 08:28
kasia: dla e2?
2 gru 08:31
kasia: tzn x= e2
2 gru 08:32
Jerzy:
Dobrze ... a jak zmienia się znak pochodnej w punkcie : x = e2 ?
2 gru 08:36
kasia: z + na −? o to chodziło?
2 gru 08:38
Jerzy:
Tak , bo na tej podstawie ustalimy jakie to jest ekstremum w punkcie x = e2
2 gru 08:39
kasia: | | 2 | |
czyli (0,e2) funkcja jest rosnąca, a od (e2, ∞) jest malejąca? ekstremum e2, |
| ? |
| | e | |
2 gru 08:44
Jerzy:
| | 2 | |
A skąd masz ekstremum dla: x = |
| ? |
| | e | |
2 gru 09:02
kasia: | | lnx | |
x podstawilam do y= |
| |
| | √x | |
2 gru 09:04
Jerzy:
Ekstremum może istnieć tylko tam, gdzie pochodna się zeruje.
| | 2 | |
Czy pochodna zeruje się w punkcie: x = |
| ? |
| | e | |
2 gru 09:06
Jerzy:
A..... policzyłaś to ekstremum ... OK. ( tylko go nazwij )
Dziedzina drugiego przykładu ?
2 gru 09:08
kasia: | | 2 | |
nie chodziło o x, współrzędna y= |
| |
| | e | |
2 gru 09:09
kasia: w drugim przykładzie nie wiem w ogóle od czego zacząć
2 gru 09:09
Jerzy:
Od dziedziny.
2 gru 09:10
kasia: (−∞,∞) ?
2 gru 09:11
Jerzy:
OK. Wiesz jak wygląda wykres tej funkcji ?
2 gru 09:13
kasia: parabola
2 gru 09:15
Jerzy:
ale całej funkcji , a nie tylko tego, co jest pod modułem.
2 gru 09:17
kasia: to nie wiem
2 gru 09:18
Jerzy:
Studiujesz ?
2 gru 09:19
kasia: tak
2 gru 09:20
Jerzy:
To zapamiętaj,że wykres funkcji: y = |f(x)I powstaje z wykresu funkcji f(x)
i odbiciu tego wszystkiego co jest pod osią OX , nad oś.
Teraz zrób szkic tej funkcji i odczytaj ekstrema i monotoniczność.
2 gru 09:23
kasia: czyli jak odbiłam nad oś to co jest pod nią, to coś się zmieniło w równaniu funkcji czy
pochodną liczę z tego co jest w wartości bezwzględnej?
2 gru 09:30
Jerzy:
W tym przykładzie nie liczymy pochodnej, bo funkcja nie jest różniczkowalna w całej
dziedzinie.
Analizujemy ja na podstawie wykresu.
2 gru 09:32
kasia: funkcja jest rosnąca w (−∞,−3) (−3, 1) (1, ∞), brak ekstremum?
2 gru 09:37
Jerzy:
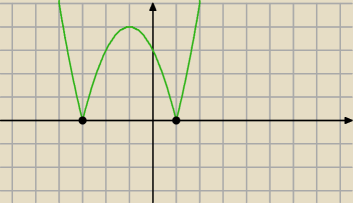
To jest wykres , teraz analizuj.
2 gru 09:40
kasia: czyli minimum x=−3 i x=1?
2 gru 09:42
Jerzy:
To minima lokalne, a maksimum lokalne ?
Popraw też monotoniczność .
2 gru 09:45
kasia: maksimum lokalne x=−1
malejąca: (−∞,−3) (−1,1) ; rosnąca: (−3,−1) (1,∞)
2 gru 09:51
Jerzy:
Teraz jest OK.
2 gru 09:56
kasia: Dziękuję
2 gru 09:57