Wyznacz dziedzinę Dżonyyy: Wyznacz dziedzinę:

	1 − x
√log
	x + 1

Dżonyyy: Wszystko pod pierwiastkiem. Najpierw robię tak:

1 − x
	>0/(x+1)
x + 1

1−x>0 X<1 D=(−∞;1) Potem:

	1 − x
log		≥0
	x + 1

I dalej nie wiem jak.. x+1≠0 x≠−1

Milo: Błąd już w pierwszym przejściu − nie możesz mnożyć razy x+1, bo nie znasz znaku tego wyrażenia Zamiast tego przejdź na iloczyn i rozwiąż (1−x)(1+x) > 0

	1−x
Drugi warunek dobry, log		≥ log1 (inaczej zapisane 0)
	x+1

	1−x
Więc		≥ 1 /(x+1)2 (można, bo kwadrat jest zawsze nieujemy, w tym wypadku dodatni bo
	x+1

mianownik nie może być zerem) (1−x)(1+x) ≥ (×+1)² Dalej rozwiąż, ale nie skracaj przypadkiem (x+1), wyłącz je przed nawias

Dżonyyy: To w pierwszym będzie: D\{1;−1}

Dżonyyy: D = R\{1;−1}

Milo: To jest nierówność, będzie x należy (−1, 1) z pierwszego warunku

Dżonyyy:

	1 − x
Kurde a dlaczego:		≥1 mnożyłaś obie strony przez (x+1)2 skąd to się
	x + 1

wzięło? dlaczego nie przez (x+1)

Dżonyyy: D = xE(−1;1) ? tak to zapisać ?

Milo: Może jeszcze nie używaj literki D, użyjesz jej do ostatecznej odpowiedzi. Pamiętaj, że nierówność zmienia znak, gdy mnożymy przez coś <0 A gdybym mnożył razy (x+1), to to jest czasem dodatnie, czasem ujemne, komplikuje mi to sprawę. Z kolei (x+1)² jest zawsze dodatnie (bo x=−1 odpada przez dziedzinę), więc wiem, że nie muszę zmieniać znaku i mogę spokojnie liczyć dalej. Przy okazji − jestem płci męskiej

Dżonyyy: (1−x)(1+x)≥(x+1)² Nie wiem jak to rozwiązać.. ehh

Dżonyyy: To wszystko wymnożyć przez siebie + wzór skr. mnożenia?

Dżonyyy: Po wymnożeniu: 0≥2x²+2x Delta = 4 x1=−2 x2=0 D = xE(−∞;−2>∪<0;+∞)

Dżonyyy: Tak?

Dżonyyy: I mam 3 dziedziny w tym momencie: x≠−1 D=R\{−1;1} D = xE(−∞;−2>∪<0;+∞) Co dalej

Milo: Pomyliłeś się przy x₁, będzie ono wynosić −1 + nierówność masz w drugą stronę, będzie <−1, 0> Na koniec musisz wziąć cześć wspólną wszystkich warunków w tym wypadku D = (−1,0> (O ile przez późną porę się gdzieś nie pomyliłem )

Milo: Dlaczego akurat taki przedział? Wyobraź sobie tę funkcję 2x² + 2x.(lub postaraj się narysować,jeśli nie uda Ci się wyobrazić). Nasze "a" jest >0, więc ramiona paraboli są w górę. My szukamy, gdzie ona jest poniżej osi OX, czyli interesuje nas przedział między miejscami zerowymi.

Milo: Bo pamiętaj, że z 2. warunku jest (−1,1), nie R\{−1,1}.

	1−x
Masz tam		> 0
	x+1

Po pomnożeniu razy kwadrat mianownika (powód ten sam jak w 3. warunku) dostajemy −x² + 1 > 0 x₁ = −1 x₂ = 1 "a" < 0, ramiona paraboli są w dół, więc nad osią będzie przedział między miejscami zerowymi, czyli (−1,1)

Dżonyyy: Dobra lecę spać, nie myślę już z rana pokminię i dodam odpowiedź

Dżonyyy:

	1 − x
Hmmm ale w tym warunku z log		chyba nie wyjdzie 2x2 + 2x
	x + 1

	1 − x
log		≥0
	x + 1

1 − x
	≥1/(x+1)2
x + 1

(1−x)(1+x)≥(x+1)² 1+x−x−x²≥x²+2x+1 1−x²−x²−2x−1≥0 −2x²−2x≥0

Jerzy: Rozwiązuj tą nierówność.

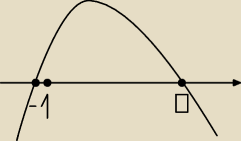
Dżonyyy: −2x²−2x ≥0 Δ=b²−4ac Δ=4 x1=0 x2=−1 D=xE<−1;0>

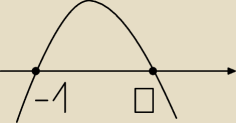
Dżonyyy: Pośpieszyłem się z rysunkiem. Tak to ofc powinno wyglądać

Jerzy: Tak.

Dżonyyy: Więc dobrze to jest , tak

Jerzy: Ostatni warunek ...tak.

Dżonyyy: A pozostałe

Jerzy:

1 − x
	> 0 i x ≠ −1
1 + x

Dżonyyy: Mam 3 warunki: 1) D=R\{−1} 2) D=xE(−1;1) 3) D=xE<−1;0> I co dalej z tym zrobić

Jerzy: Ustalić część wspólną tych trzech zbiorów.

Dżonyyy: Część wspólna więc wyjdzie: D=xE(0;1>

Jerzy: A skąd masz warunek 3) x ∊ <−1;0>

Dżonyyy: Z nierówności: −2x2−2x≥0 , tam przy rysunku paraboli tak mi wyszło i powiedziałeś, że jest ok

Jerzy: Racja .. przegapiłem to. Ale popraw ostateczny wynik.

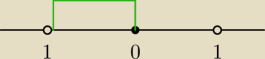
Jerzy: Tutaj masz trzy warunki spełnione jednocześnie.

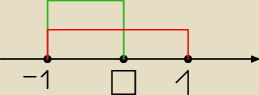
Dżonyyy: Ale 1 jest wyłączona bo R\{−1} To nie powinno tak wyglądać?

Dżonyyy: * −1

Jerzy: Patrz rysunek 12:24

Dżonyyy: Przy −1 otwarte kółeczko

Dżonyyy: Widzę. A co się stało z warunkiem: D=xE(−1;1)

Jerzy: To już jest rysunek rozwiązania ... wszystke: x > 0 odpadły z warunku: x ∊ <−1;0>

Dżonyyy: A więc ostateczny wynik to: D=xE(−1;0>, tak

Dżonyyy:

Jerzy: Tak.

Dżonyyy: Ok. Bardzo dziękuję za pomoc Jerzy