Geometria
5-latek: Zadanie nr 1 . Uzasadnij ze jesli prosta c przecina prosta b i prosta b jest rownolegla do
prostej a to prosta c przecina prosta a
Zadame nr 2 .
Czy mozna tak dobrac polozenie n punktow aby wyznaczaly one dokladnie n prostych (n>3
1 gru 10:26
===:
zadanie nr 1 tak całkiem to prawdziwe nie jest
coś w treści chyba pominąłeś
1 gru 11:05
5-latek: Czesc
....to prosta c przecina
rownież prosta a .
1 gru 11:08
Janek191:
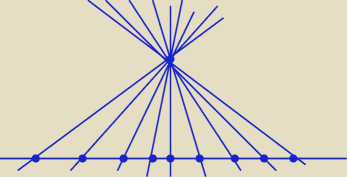
z.2
Tak. Np. dla n = 10
1 gru 11:09
5-latek: Witaj
To oznacza ze musza one nalezec do tej samej prostej .
1 gru 11:12
===:
...
1 gru 11:19
Jerzy:
... tu zapewne chodzi o płaszczyznę
1 gru 11:22
Janek191:
@ 5 − latek
a,b,c leżą na płaszczyźnie
1 gru 11:23
5-latek: Pewnie tak bo to zadanie z 1 klasy liceum
mam tutaj wykorzystac relacje rownoleglosci prostych .
1 gru 11:24
===:
albo tylko prostopadłe ... bez przecinania
1 gru 11:33
5-latek: Dobrze .
Juz wiem o co biega
Muszse wtutaj wykorzystac 3 warunek rownoleglosci prostych
Dla kazdej trojki prostych a b c aIIb i bIIc to aIIC i zrobic dowodem nie wprost .
1 gru 11:41