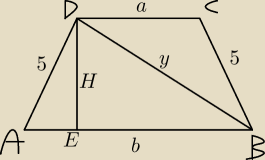
Wykaż, że przekątna trapezu wpisanego w koło jest prostopadła do ramienia. benc: Czy ktoś mógłby mi wytłumaczyć jak udowodnić, że przekątna trapezu wpisanego w koło jest prostopadła do ramienia? Zadanie potrafie rozwiązać ale nie chciałbym stracić punktów przez taką rzecz na sprawdzianie. Przekątna y= 12 cm Odcinek |EB|= 144/13 cm Wysokość H= 60/13 cm Ramiona = |AD| = |CB| = 5 cm Wydaje mi się, ze trzeba jakoś wykorzystać informacje (a+b)/2 = 144/13 cm. Nie wiem jak to ubrac w słowa, prosiłbym o pomoc!

benc: Oczywiście b = |AB|

Mila: Podaj całą treść.

benc: W trapezie równoramiennym dane są: długość ramienia 5 cm, długość przekątnej 12 cm i długość wysokości trapezu 60/13 cm. Oblicz: a) pole trapezu b) pole koła opisanego na tym trapezie. Wszystko obliczyłem, odpowiedzi mi się zgadzają. Z tyłu książki jest wskazówka do podpunktu b): wykaż, że przekątna trapezu jest prostopadła do ramienia. Tylko na tym mi zależy.

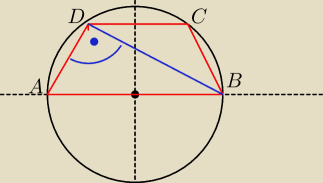
Milo: AB jest średnicą tego okręgu, więc kąt o którym mowa jest kątem wpisanym opartym na średnicy.

benc: Nie bardzo rozumiem o którym kącie mowa? I dlaczego AB jest średnicą bo zastanawiam się jak to wykazać.

5-latek:

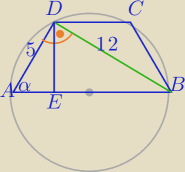
Mila: Przekątna trapezu wpisanego w okrąg jest prostopadła do ramienia, jeżeli AB jest średnicą (wtedy kąt C=90^o jako wpisany oparty na średnicy). Do obliczenia pola koła potrzebny jego promień. Zatem musisz obliczyć AE.

	25
|AE|=
	13

|AB|=13 Jeżeli zauważysz , że trójkąt o bokach 5,12,13 jest Δprostokatnym, to masz dł. promienia.

	60   13		12
Jeżeli nie zauważysz , to liczysz np. sinA=		=
	5		13

Z tw. sinusów:

12
	=2R
sinA

12
	=2R
12   13

2R=13 I masz to samo.

5-latek: Dobry wieczor Milu czy juz jestes zdrowa ? Ostatnio pisalas ze bylas przeziebiona .

benc: Oh w pitagorasie 25/13 − 3600/13 = x² zamiast minusa dałem plus. Chyba pora iść spać, dzięki za tak wyczerpującą odpowiedź i sorry za taki głupi kłopot.