Trójkąty i funkcje RATUJCIE
Kinia:
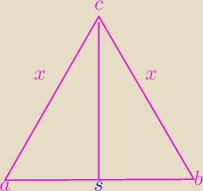
Odcinek AB o końcach A(−1,1) B (3,−1)
jest podstawą trójkąta równoramiennego ABC którego pole jet równe 15.Wyznacz wspołrzedne C
30 lis 22:45
Kinia: PROSZĘ O POMOC NIE WIEM JAK SIE ZA
TO ZABRAĆ OBLICZYŁAM WYSOKOŚĆ I DŁUGOŚĆ S I DŁUGOŚĆ AB I X I NIE WIEM

30 lis 22:52
majka: jesli masz współrzedne S i długosc h to C=(xs;ys+h) bo jest dokładnie nad S
30 lis 22:58
Kinia: czyli wyszłoby (proszę mnie sprawdzić) S(1,0) H= 3
√5 wiec C= (1+3
√5,0)

?
30 lis 23:08
Metis: Oblicz teraz pole i sprawdź czy sie zgadza
Kinia 
30 lis 23:11
majka: a nie chyba ci zle powiedzialam zmylona rysunkiem C nie jest nad S bo to przechylony trójkat
30 lis 23:17
Kinia: podstawa to 2√5 wysokość to 3√5
2√5 * 3√5 \2=15 pole się zgadza ale czy na pewno punkt C jest dobry?
30 lis 23:24
Kinia: majka proszę pomóż

30 lis 23:25
Metis: Będą dwa takie punkty

30 lis 23:29
Mila:
|AB|=
√22+42=
√20=2
√5
√5*h=15 /*
√5
5h=15
√5
h=3
√5
S=(1,0) wsp. spodka wysokości
C=(x,y)
SC⊥AB
prosta AB:
| | −1−1 | | 1 | |
y=a*x+b, gdzie a= |
| =− |
| |
| | 3+1 | | 2 | |
prosta h:
y=2x+b i S∊h ⇔0=2*1+b, b=−2
h: y=2x−2
|SC|=3
√5
√(x−1)2+(y−0)2=3
√5 i y=2x−2
x
2−2x+1+(2x−2)
2=9*5 rozwiąż
x=−2 lub x=4
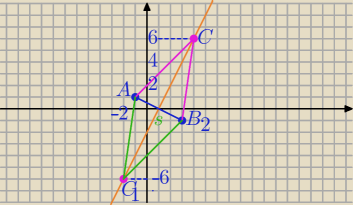
stąd y=2*(−2)−2=−6 lub y=2*4−2=6
C
1=(−2,−6) lub C
2=(4,6)
30 lis 23:30
Kinia: Dziękuje BAAARDZOOO

30 lis 23:31
Mila:

30 lis 23:32
Metis: 
30 lis 23:33
Metis: Milu jak samopoczucie


?
30 lis 23:34
Mila:
Może być. Dziękuję za zainteresowanie.

30 lis 23:35
Metis: Może być?

Coś się stało
Milu?
30 lis 23:36
Eta:
S(1,0)
AB: y=−0,5x+0,5 to CS : y= 2(x−x
S)+y
S ⇒ h: y=2x−2 więc C(x, 2x−2)
|AB|= 2
√5 to h=3
√5
Odległość punktu C od prostej AB = h=3
√5
AB: w postaci ogólnej: x+2y−1=0 i C(x, 2x−2) i d=h= 3
√5
| | |x+2(2x−2)−1| | |
zatem: |
| =3√5 |
| | √5 | |
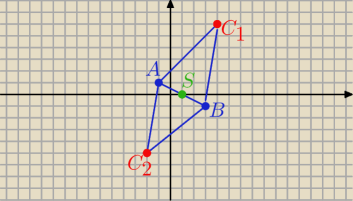
|5x−5|= 15 ⇒ |x−1|= 3 ⇒ x= 4 lub x= −2 to y= 2*4−2= 6 lub y= 2*(−2)−2= −6
odp:
C1(4,6) lub C2 (−2, −6)
30 lis 23:37
Kinia: Środek AB − współrzędne to (0,1) a nie (1,0) a tak to chyba dobrze wyszło

1 gru 00:48
Kinia: przepraszam dobrze wszystko ja nie myśle haha nie patrzcie na moje odp
1 gru 00:50
:::=:=:=:::
S(1,0)
1 gru 00:51
 Odcinek AB o końcach A(−1,1) B (3,−1)
jest podstawą trójkąta równoramiennego ABC którego pole jet równe 15.Wyznacz wspołrzedne C
Odcinek AB o końcach A(−1,1) B (3,−1)
jest podstawą trójkąta równoramiennego ABC którego pole jet równe 15.Wyznacz wspołrzedne C

 ?
?



 |AB|=√22+42=√20=2√5
|AB|=√22+42=√20=2√5




 ?
?

 Coś się stało Milu?
Coś się stało Milu?
 S(1,0)
AB: y=−0,5x+0,5 to CS : y= 2(x−xS)+yS ⇒ h: y=2x−2 więc C(x, 2x−2)
|AB|= 2√5 to h=3√5
Odległość punktu C od prostej AB = h=3√5
AB: w postaci ogólnej: x+2y−1=0 i C(x, 2x−2) i d=h= 3√5
S(1,0)
AB: y=−0,5x+0,5 to CS : y= 2(x−xS)+yS ⇒ h: y=2x−2 więc C(x, 2x−2)
|AB|= 2√5 to h=3√5
Odległość punktu C od prostej AB = h=3√5
AB: w postaci ogólnej: x+2y−1=0 i C(x, 2x−2) i d=h= 3√5
