Monotoniczność i ekstrema.
Esgath: Mam duży problem z zadaniami tego typu
Znależć wartość najmniejszą i największą funkcji w przedziale <2;4>
muszę napisać to w taki sposób bo wychodzi dość niewyrażnie :
f(x)= (x4) : (x3 − x)
Dziedzina : x należy do (− ∞; −1) u (−1;0)u(0;1)u(1; ∞)
Więc liczę pochodną i otrzymuję równanie :
0 = x2(3x2)(x2−1)(3x2 − 1)
Wyznaczam miejsca zerowe kilka nie należy do dziedziny
Należą : x=4 i x= √13 x= − √13
I teraz pytanie jak mam to narysować, a jest dodatnie czy nie bo nie jestem już niczego pewny z
tymi pochodnymi.
29 lis 20:02
Esgath:
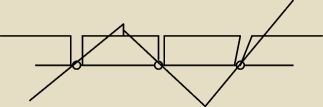
Czy to mniej więcej tak wygląda ? przepraszam nie umiem korzystać z tej opcji

29 lis 20:05
Jerzy:
Liczysz wartość na końcach przedziału i ewentualne ekstrema lokalne
w podanym przedziale.
29 lis 20:05
Janek191:
| | x4 | | x3 | | x3 | |
f(x) = |
| = |
| = |
| |
| | x3 − x | | x2 − 1 | | ( x −1)*(x + 1) | |
Df = ℛ \ { 0, − 1, 1 }
| | 3 x2*(x2 − 1) − x3*2x | |
f '(x) = |
| |
| | (x −1)2*(x + 1)2 | |
| | 3 x4 − 3 x2 − 2 x4 | | x4 − 3 x2 | |
f '(x) = |
| = |
| = 0 ⇔ |
| | (x −1)2*(x +1)2 | | (x −1)2*(x + 1)2 | |
⇔ x = −
√3 lub x =
√3
29 lis 20:12
Janek191:
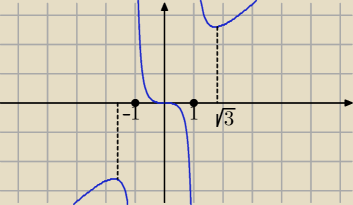
29 lis 20:15
Esgath: Dziękuje

29 lis 20:21
Janek191:
ymin = f(2) =
ymax = f(4) =
29 lis 20:27
 Czy to mniej więcej tak wygląda ? przepraszam nie umiem korzystać z tej opcji
Czy to mniej więcej tak wygląda ? przepraszam nie umiem korzystać z tej opcji

