Zbiory opisane równaniami (liczby zespolone) BiednyStudent: Jak wyglądają zbiory opisane równaniami: |(1+i)z+(1−i)| = 1 |z−2|=|z−3i| |z−1| = 2|z| Proszę o pomoc. Podstawiając za Z = x + yi coś tam mi wychodzi, ale chyba coś jest nie tak

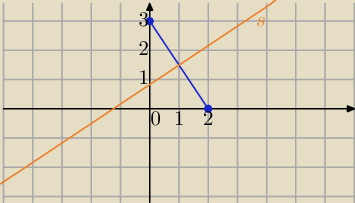
Mila: 2) |z−2|=|z−3i| punkty symetralnej odcinka o końcach : (2,0) i (0,3) (x−2)²+y²=x²+(y−3)² x²−4x+4+y²=x²+y²−6y+9⇔ −4x+4=−6y+9 6y=4x+5

	2		5
y=		x+
	3		6

Mila: c) |z−1| = 2|z| z=x+iy, gdzie x,y∊R |x+iy−1|=2|x+iy| √(x−1)²+y²=2*√x²+y² x²−2x+1+y²=4*(x²+y²) ⇔x²−2x+1+y²=4x²+4y² 3x²+3y²+2x−1=0 /:3

	2		1
x2+y2+		x−		=0
	3		3

	1		1		3
(x+		)2−		+y2−		=0
	3		9		9

	1		4
(x+		)2+y2=
	3		9

	1		2
okrąg o środku (−		,0) i r=
	3		3