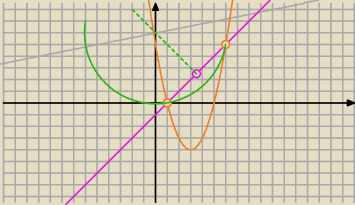
równanie okręgu Skynet: Środek okręgu należy do prostej l, o równaniu x−5y−30=0, a okrąg przechodzi przez punkty wspólne prostej k:x−y−1=0 i paraboli y=x²−6x+5. Napisz równanie okręgu i oblicz pole trójkąta równobocznego opisanego na tym okręgu.

===:

Janek191:

	1
l : x − 5 y − 30 = 0 ⇒ 5 y = x − 30 ⇒ y =		x − 6
	5

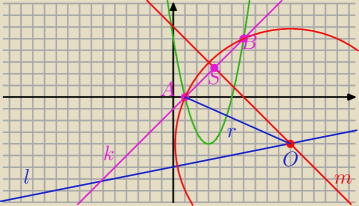
k : x − y − 1 = 0 ⇒ y = x − 1 y = x² − 6 x + 5 więc x − 1 = x² − 6 x + 5 x² − 7 x + 6 = 0 ( x − 6)*( x − 1) = 0 x₁ = 1 x 2 = 6 y₁ = 0 y₂ = 5 A = ( 1, 0) B = ( 6, 5)

	1 + 6		0 +5
S = (		,		) = ( 312 , 212)
	2		2

Prosta prostopadła do k : y = − x + b 2,5 = −3,5 + b ⇒ b = 6 m :y = − x + 6 ======== Punkt wspólny z prostą l :

	1
− x + 6 =		x − 6
	5

−1,2 x = − 12 x = 10 y = − 4 O = ( 10, − 4) =========== r² = I OA I² = 6² + 4² = 52 ⇒ r = 2√13 Równanie okręgu ( x − 10)² + ( y + 4)² = 52

Skynet: dzięki wielkie

Janek191:

	2
r =		h
	3

h = 1,5 r = 3√13

	√3		2
a *		= 3√13 / *
	2		√3

	6 √13		6 √39
a =		=		= 2√39
	√3		3

Pole Δ równobocznego

	a2 √3		4*39 *√3
P =		=		= 39 √3 [ j2]
	4		4

Janek191: Poprawka I OA I² = ( −9)² + 4² = 81 + 16 = 97 więc równanie okręgu ( x − 10)² + ( y + 4)² = 97

Janek191: Poprawka − cd. r = √97 h = 1,5 r = 1,5 √97

	√3
a*		= 1,5 √97
	2

	3 √97
a =		= √97*√3
	√3

a² = 97*3 = 291 Pole Δ równobocznego :

	a2 √3		291 √3
P =		=		[j2]
	4		4

==================================

skynet: w odpowiedzi jest pole trójkąta 291√3

Janek191: r = √97 h = 3 r = 3 √97

a √3
	= 3 √97
2

a √3 = 6 √97 a = √97*2 √3 a² = 4*97*3 =4* 291

	a2 √3		4*291 √3
P =		=		= 291 √3
	4		4

=================================== Przez pomyłkę obliczyłem pole Δ wpisanego w ten okrąg. Przepraszam. O tej porze powinienem już iść spać