Ciagi arytmetyczne i tw. cosinusow sssss: Miary katow trojkata tworza ciag arytmetyczny i dlugosci bokow tworza ciag arytmetyczny, jaki to trojkat?

paziówna: a jest taki trójkąt?

sssss: Moze i nie ma, ale trzeba to jakos udowodnic

paziówna: ech... różnica w ciągu arytm (boków) wyszła mi 0, nie wiem, czy to ja zrobiłam błąd, czy co... ale po tym zrezygnowałam

sssss: Rownoboczny odpada. Prostokatny tez, bo jesli dobrze mysle to jedynymi katami ktore tworza ciag arytmetyczny sa 30,60,90. A wtedy boki nie tworza ciagu aryt. . Nauczyciel mowil ze to sie rozwiazuje wlasnie z tw. Cosinusow, ktorego jeszcze nie mialem, i dlatego to takie dodatkowe. Bogdanie , Eto moze Wy cos wymyslicie?

Sabin: paziówna, dobrze Ci wyszło, ciąg postaci a,a,a jest jak najbardziej ciągiem arytmetycznym... Trójkąt wychodzi równoboczny. Pokazać?

sssss: O! Jesli moglbys/abys

paziówna: no to to jest równoboczny

Sabin: Oznaczam boki jako a, a+r, a+2r, zaś kąty jako α, α+x, α+2x Zakładam, że r oraz x > 0, to (chyba) nie powinno zmniejszyć ogólności rozwiązania. Wtedy z sumy kątów dostajemy 3α + 3x = 180, czyli α + x = 60 − mamy jeden z kątów. Ponieważ naprzeciw dłuższego boku mamy większy kąt, to naprzeciw boku a mamy kąt α, boku a+r kąt α+x = 60, zaś boku a+2r kąt α+2x (tu korzystam z założenia r,x > 0). Wtedy korzystając z tw. cosinusów: (a+r)² = a² + (a+2r)² − 2a(a+2r)cos60 wygląda strasznie, ale po wykorzystaniu wzorów skróconego mnożenia i uporządkowaniu bardzo dużo rzeczy się uprości, skróci i stąd dostaniemy 3r² = 0 czyli r=0. Nasz trójkąt ma więc boki postaci a,a,a i jeden kąt jest 60, więc musi być to trójkąt równoboczny.

paziówna: a tu masz tw cosinusów, jeśli jeszcze nie rzuciłeś okiem: https://matematykaszkolna.pl/strona/543.html

Eta: a,a,a −−− to r=0 60^o, 60^o, 60^o −−− r=0 więc równoboczny

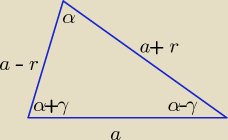
Bogdan: (α − γ) + α + (α + γ) = 180^o ⇒ α = 60^o Z twierdzenia kosinusów: a² = (a − r)² + (a + r)² − 2(a − r)(a + r)cosα

	1
a2 = a2 − 2ar + r2 + a2 + 2ar + r2 − 2(a2 − r2)*
	2

0 = a² + 2r² − a² + r² ⇒ 3r² = 0 ⇒ r = 0 a − 0 = a, a + 0 = a Jedynym trójkątem spełniającym warunki zadania jest trójkąt równoboczny.

sssss: Dziekuje bardzo za pomoc myslalem ze ciag a,a,a nie jest ciagiem arytmetycznym, a tu jednak tak czy inaczej nie poradzilbym sobie bez Was . Jeszcze raz dziekuje , i zycze dobranoc