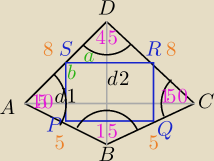
Deltoid Piotr: W deltoidzie ABCD połączono środki boków, tworząc czworokąt PQRS. Oblicz obwód prostokąta PQRS, wiedząc, że |<A| = |<C| = 150°, |<D|=45° oraz |AB|=5, |AD|=8. Załóżmy, że SR i PQ = a, SP i RQ = b.

	1		1
a =		d1, b =		d2.
	2		2

Z twierdzenie cosinusów obliczyłem, że:

	√2
d12 = 64+64−128*
	2

d₁² = 128−64√2 = 64(2−√2)

	√3
d22 = 25+64 − 80* (−		) (bo cosinus 150° = −sin60°)
	2

d₂² = 89+40√3 Dobre zastosowałem tutaj myślenie? Jeżeli tak, to

	√64(2−√2)
a =
	2

	√89 + 40√2
b =
	2

Dobrze myślę jak dotąd?

Karolina : Pomożecie?

Eta: z twierdzenia kosinusów w trójkątach ASP i DSR

	√3		√2
b2=42+2,52+2*4*2,5*		a2=42+42−2*4*4*
	2		2

b=........... a=................... Obwód : 2a+2b=............

Mila: Nie podobają mi się te dane. Skoro kąt ma miarę 15 ^o to AB i BC powinny być dłuższe niż 5. Sprawdź w książce ( jakiej, może mam) czy dobrze przepisałeś.

Eta: Witaj Milu Nie czytałam treści

Mila: Witaj Eto. | AC| nie zgadza się z górnego i dolnego Δ, prawda? Jakoś Piotr nic nie odpowiada.

Eta: Dokładnie

Piotr: Przepraszam za brak odzewu; taką treść dokładnie mam w zadaniu, nie jest ono z podręcznika tylko przygotowane przez nauczyciela. Rysunek sam robiłem, ale jeżeli mówicie że treść jest blędna to prawdopodobnie nauczyciel mógł się pomylić. Dzięki wielkie za odpowiedź, powiecie dlaczego wg. was treść jest nieprawidłowa? Pójdę z tym jutro i pogadam o tym zadaniu

an:

	AB
Jeżeli miałyby pozostać kąty		≈2,93 czyli prawie 3 razy, tu 1,6 i to odwrotnie
	AD