Pole powierzchni Nadii: Kąt przy wierzchołku A równoległoboku ABCD jest równy α, a krótsza przekątna jest prostopadła do boków AB i CD. Objętość bryły powstałej przez obrót równoległoboku wokół boku AB jest równa V. Wyznacz pole powierzchni tej bryły.

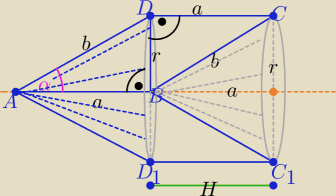
Eta: V(bryły)= V (walcaDD₁CC₁) P_c(bryły)= P_b(walca)+2P_b(stożka) H=a , r=e, l_st= b V=πr²*H , r=b*sinα , a=H= b*cosα

	V
V= πb3sin2α*cosα ⇒ b= 3√
	πsin2α*cosα

P_c=2πrH+2πrl= 2πr(H+l) = 2πbsinα(bcosα+b)= 2πb²sinα(cosα+1)=......

	V2
podstaw za b2= 3√
	π2sin4α*cos2α