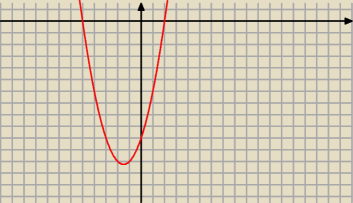
Potrzebne. Patka: 1.Dana jest funkcja f(x)= x² +3x−10 a) oblicz współrzędne wierzchołka i jej miejsca zerowe b)sporządź wykres funkcji c)napisz jej postać kanoniczną d)napisz jej postać iloczynową 2.Dane są przedziały A=(−∞ ; 7) oraz B= <5;10>. Wyznacz ich sumę, iloczyn i obie różnice. 3. c) Oblicz liczbę, której 0,6 wynosi 0,06

Jack: 1. y = x² +3x − 10 x² + 3x − 10 = 0 Δ = 9 + 40

	3		49
xw = −		, yw = −
	2		4

√Δ = 7 x₁ = ... x₂ = ...

Patka: a dalej?

Patka: rozwiąże ktoś do końca i napisze o co chodzi?

Jack: a sama? coś? coś niecoś? cokolwiek?

Patka: a nie możesz tej funkcji chociaż do końca rozwiązać?

Jack: ax² + bx + c gdy Δ > 0 to

	−b−√Δ
x1 =
	2a

	−b+√Δ
x2 =
	2a

w naszym przypadku to zachodzi, tzn Δ > 0 zatem?

Patka: ale co do czego? bo ja już ie wiem. nie możesz rozwiązać po kolei ? proszę.

Jack: y=x² + 3x − 10

	3		49
wierzcholek −−−−> W(−		, −		) (obliczony w poscie 20;00)
	2		4

	−3 − 7
x1 =		= − 5
	2

	−3 + 7
x2 =		= 2
	2

(to sa miejsca zerowe czyli 2 i − 5) zatem nasze rownanie to y=(x−2)(x+5) (to jest postac iloczynowa) oraz wykorzystujac wierzcholek

	3		49		3		49
y = (x−(−		))2 + (−		) = (x+		)2 −
	2		4		2		4

a to z kolei jest postac kanoniczna.