To co w poleceniu Eszmon: Wyznacz zbiór środków cięciw paraboli y=3x² przechodzących przez punkt P=(0,2)

Eta: Cięciwy są postaci y=ax+2 Końce cięciw to A(x₁, y₁) , B(x₂,y₂) gdzie A i B to punkty wspólne z parabolą

	x1+x2		y1+y2
zatem środki cięciw to punkty :S(		,		)
	2		2

aby otrzymać współrzędne punktów A i B rozwiązujemy układ równań

⎧	y= 3x2
⎩	y=ax+2	⇒ 3x2−ax−2=0 ,Δ=a2+24 >0 to a∊R

	a		x1+x2		a
ze wzorów Vietea x1+x2=		to		=
	3		2		6

	y1+y2		x1+x2		a2
zatem		= a*		+2 =		+2
	2		2		6

	a		a2
zbiór takich środków S(		,		+2)
	6		6

tworzą parabolę y= 6x²+2

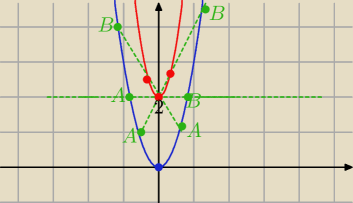
Mila: y=3x² i y=m*x+2 A,B− Końce cięciw leżą na prostej i na paraboli⇔ 3x²−mx−2=0 Δ>0 Δ=m²+4*3*2=m²+24 >0 dla każdego m∊R

	m−√Δ		m+√Δ
x1=		lub x2=
	6		6

	m−√Δ		m+√Δ
y1=m*		+2 lub y2=m*		+2
	6		6

A=(x₁,y₁), B=(x₂,y₂) środek cięciwy AB S(x_s,y_s)

	m−√Δ   m+√Δ   + 6   6		2m		m
xs=		=		=
	2		12		6

	m−√Δ   m−√Δ   m* +2+m* +2   6   6		m2
ys=		=		+2
	2		6

	m		m2
x=		i y=		+2 , m∊R − równanie parametryczne krzywej
	6		6

================================================] teraz przekształcamy m=6x

	1
y=		*(6x)2+2
	6

y=6x²+2 ======= Posprawdzaj rachunki

Eta:

Eta: