geo analityczna Lipa: Na prostej o rownaniu x+5y−20=0 znajdz taki punkt P o dodatnich wspolrzednych, ze iloczyn ich odleglosci punktu P od osi ukladu wspolrzednych jest najwieksza z mozliwych.

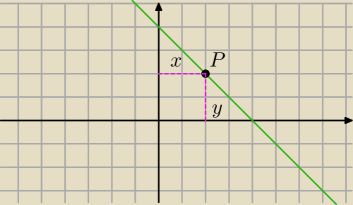
Jerzy: Teraz szukasz maksymalne pole prostokąta o bokach : x i y

Lipa:

	1
y=−		x+4
	5

	1
P(x,−		x+4)
	5

	1		−1
P=x*y=x*(−		x+4)=		x2+4x
	5		5

	−b		−2		5
p=		=U{−4}{		=−4*(−		)=10
	2a		5		2

−1
	*10+4=2
5

P(10,2)

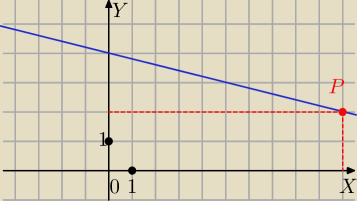
Janek191: x + 5 y − 20 = 0 ⇒ y = − 0,2 x + 4 P = (x, y) = ( x, −0,2 x + 4) Iloczyn odległości P od osi: i(x) = x*( − 0,2 x + 4) = −0,2 x² + 4 x

	− 4
p =		= 10 to imax = q = −0,2*100 + 40 = 20
	−0,4

P = ( 10, 2) =========

Lipa: mozna bylo tez skorzystac z pochodnej

	2
P'(x)=−		x+4
	5

−2
	x+4=0
5

−2
	x=−4
5

x=10 f ↗ dla x∊(−∞,10) czyli f_max=10

−1
	*10+4=−2+4=2
5

P(10,2)

Jerzy: Można było, ale po co ?

relaa: Gdzie dziedzina?

Lipa:

	−1
x>0 ⋀		x+4>0
	5

	−1
		x>−4
	5

x<20 x∊(0,20)

jc: x, y ≥ 0 400 = (x+5y)² ≥ 20 xy, równość zachodzi dla x=5y, czyli dla y=2, x=10. Wtedy xy = 20.

relaa: Trochę też, jedziesz bez pomyślunku. Masz postać iloczynową więc z niej już możesz wyliczyć dla jakiego argumentu otrzymasz ekstremum.

	x1 + x2
p =		.
	2