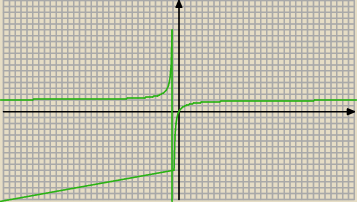
Wykres funkcji kasia: Podaj ekstrema funkcji Wyznacz dziedzinę funkcji. Podaj dla jakich x funkcja ma ciągłe kawałki. znajdź dla funkcji największą wartość w przedziale (−1,∞> Proszę o pomoc

kasia: Chodzi tutaj o funkcję f(x)=(2x)/(x+1)

Jerzy: Zacznij od dziedziny, potem policz pochodną.

kasia: Jest to funkcja f(X) = (−2)/x przesunięta o (−1,2) czy dziedziną bedzie D=R\{−1} ?

Adamm:

	2
f(x)=2−
	x+1

	2
f'(x)=		≠0 dla każdego x
	(x+1)2

x∊ℛ\{−1} funkcja jest ciągła w całej swojej dziedzinie, ponieważ jest elementarna

Jerzy:

	2(x+1−1))		2(x+1)		1		1
Albo: f(x) =		=		−		= 2 −
	x+1		x+1		x+1		x+1

i już widać,ze: 1) x ≠ −1 2) (−∞,−1) U ( −1,+∞) 3) nie osiaga wartośći największej w tym przedziale

kasia: Dziękuję, a funkcja będzie rosnąca w przedziale (−∞;−1) U (−1;+∞) ? Czy nawiasy beda ostre?

Kacper: Funkcja jest rosnąca w każdym z przedziałów (−∞,−1), (−1,+∞). W dziedzinie nie jest rosnąca.

kasia: Dziękuję. Pochodna tej funkcji wyszła mi f'(x) = 2/ (x+1)²

kasia: Czy to jest dobrze?

kasia: Jak teraz wyliczyć z tego ekstrema?

Jerzy: Dobrze .... i widzisz ,że pochodna jest różna od zera , a więc nie ma ekstermów.

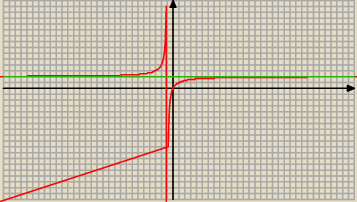
kasia: Dzięki, a czy jeżeli zielona linia to liczba (e) . (w rzeczywistości zielona linia nie nachodzi ona na hiperbole ) to czy wzór tej funkcji nadal bedzie rowny f(x)= (2x)/(x+1) ?

Adamm: jeśli zielona linia jest liczbą Eulera to wzór będzie inny

Jerzy:

	2x
Zielona linia to : y = 2 , asymptota pozioma funkcji f(x) =
	x+1

kasia: A czy ktoś pomoże mi jakby wygladal taki wzor z e ?

kasia: Czyli wzor ogolny sie jednak nie zmieni ?

Jerzy: Co znaczy z e ?

Jerzy:

	1
Np. funkcja: f(x) =		+ e ma asymptotę poziomą : y = e
	x

kasia: Wyżej narysowałam na wykresie zielona linie jest to linia oznaczona liczbą e . czy jesli ta linia dojdzie do wykresu funckji f(x)= 2x/(x+1) to czy wzor ogolny tej funkcji się zmieni na np. f(x) = ex / (x+1) ?

kasia: Czy zatem bedzie to funkcja f(x) = −2/ x przesunięta o ( −1,e ) ?

Jerzy:

	1		1 + e(x+1)		ex+2
f(x) = − [		+e] = −[		]= −
	x+1		x+1		x+1

	1
To funkcja f(x) =		przesunięta o wektor: v = [−1,e]
	x

Jerzy:

	1
Tzn: funkcja: f(x) = −		przesunięta o ten wektor.
	x

kasia: Dzięki wielkie, ale ta funkcja też nie bedzie miala ekstremum, dobrze licze?

Jerzy: Nie będzie miała ekstermów , będzie miała tylko granicę: g = e przy x → +/− ∞

kasia: bo wychodzi mi, że pochodną funkcji f(x) = ²_x+1 + e to 2e ? chyba źle licze. moglbys mi jeszcze tylko pomoc obliczyc ta pochodna ?

kasia: tak i teraz największą wartością w przedziale (−1,∞> będzie liczba 'e' ?

Jerzy:

	e(x+1) − (ex+2)		e − 2		2 − e
f'(x) = −		= −		=
	(x+1)2		(x+1)2		(x+1)2

Jerzy:

kasia: Dzięki. czyli teraz tą najwieksza wartoscia bedzie liczba e czy nadal nie bedzie najwiekszej waetosci ?

Jerzy: Ta funkcja nie osiąga ekstremum , bo pochodna jest różna od 0 dla każdego x należącego do dziedziny.

kasia: tak, tak ekstremum nie bedzie, ale chodzi mi o to czy w przedziale (−1,∞> będzie najwieszka wartosc?

Jerzy: Dziecko, największa lub najmniejsza wrtość to właśnie ekstremum !

kasia: Dzieki i sory za klopot

Jerzy: Nie ma problemu ...grunt żebyś to zrozumiała.

Adamm: aha, czyli dla x∊<0;2> też nie ma najmniejszej ani największej wartości

Jerzy: Nie myl kolego najmniejszej lub największej wartości funkcji w przedziale , z ekstremami lokalnymi funkcji. Funkcja f(x) = x² też ma wrtość najmniejszą i największą w przedziale <0,2>, a nie posiada ekstremów.

Jerzy: Oczywiście miałem na myśli f(x) = x³ ( palcówka)

Adamm: Jerzy, patrz na swój post 13:34

Jerzy: I co ? , gdzie tam jest mowa o przedziale ?

Adamm: w poście 13:33

Jerzy: 13:33 nic nie pisałem

kasia: czyli jednak będzie największa wartość w przedziale (−1,∞> ?

Adamm: odpowiadałeś na post, zresztą musimy ustalić co uznajemy za przedział (−1;∞>

Janek191:

	2 x
f(x) =
	x + 1

Jerzy: Adaś.. skończmy tą dyskusję, co innego eksteremum ( lokalne lub globalne) , a co innego warrtość ekstremalna w przedziale.

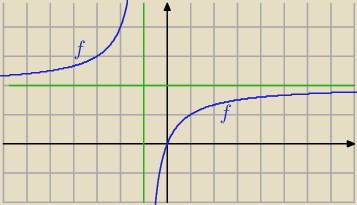
Jerzy: Janku ... ten wykres był już na poczatku tego wątku

Adamm: Jerzy, właśnie nie, wprowadziłeś w błąd i teraz się tego wypierasz

kasia: Chodzilo mi o najwieksza wartość funkcji w przedziale (−1;∞> i wnioskowalam, ze bedzie to e, poniewaz hiperbola nie przekroczy tej wartości więc bedzie ona najwieksza. Czyli odpowiedź Jerzego jest poprawna czy nie ?

Janek191: Jakiś niezbyt udany ten wykres Pozdrawiam

Jerzy: Kasiu ... po pierwsza przedział zapisuj (−1,+∞) ( przedział otwarty !) Po drugie ... y = e asymptota , tan wartość funkcji zbliża się do e , ale nigdy jej nie osiąga !

Adamm: co znaczy (−1;∞> ja nie znam takich przedziałów

kasia: byc moze pani w szkole pomylila sie z tym przedzialem, tez przedział domkniety wydawal mi sie dziwny przy nieskonczonosci. Ok nie dojdziemy do poprawnej odpowiedzi wiec zakonczmy temat bo niepotrzebnie sie spieracie pozdrawiam i dziekuje za pomoc

Jerzy: Już to chyba wyjaśniliśmy

Jerzy: Ta funkcja nie osiąga ekstremów ! ( nie ma maksimun i nie ma minium )

Adamm: Jerzy, nie zaczynaj bo mnie szlak trafi koniec tematu

Jerzy: szlag

kasia: Juz zglupialam, tez uwazam ze ta funkcja nie ma ekstremow, bo pochodna sie nie zeruje. czy Adammm sadzi inaczej ?

Jerzy: Kasiu... Adamm podał konkretny przedział <0,2> i w tym przedziale funkcja osiąga wartość maksymalną, ale to nie jest ekstremum lokalne funkcji !

kasia: dzieki chlopaki i przepraszam za ten dziwny przyklad

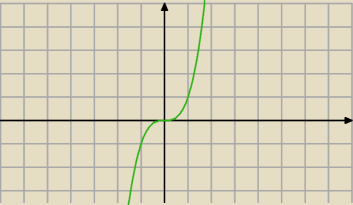
Jerzy: Czy ta funkcja osiąga ekstremum ?