Jack:
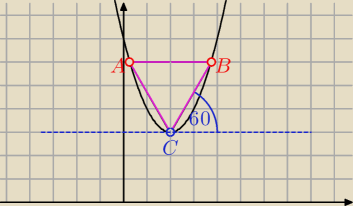
parabola
y=x
2 − 4x + 7
wiemy, ze jeden z wierzcholkow trojkata to wierzcholek paraboli, zatem policzmy wierzcholek
paraboli.
f(p) = 2
2 − 4*2 + 7 = 3
zatem jeden z wierzcholkow trojkata (nazwijmy go C ma wspolrzedne (2,3).
Prowadzac prosta rownolegla do osi OX przechodzaca przez punkt C, mozemy wyznaczyc
rownanie prostej CB.
wspolczynnik kierunkowy prostej = tg α
u nas tg 60 =
√3
zatem a =
√3
wspolrzedne C(2,3) znamy, zatem prosta przechodzaca przez punkty C i B ma rownanie
y =
√3(x−2)+3 =
√3x − 2
√3 + 3
no i teraz porownajmy kiedy przetnie sie ta prosta i parabola.
√3x − 2
√3 + 3 = x
2 − 4x + 7 (wyjda nam 2 punkty, jednym z nich jest C, a drugim B)
i stad znamy punkt B, a nastepnie wierzcholek A poznamy np.
robiac tak samo czyli tym razem bierzemy katy 60+60 = 120 stopni
albo porownujac odleglosci
|AB| = |AC|
i tyle.
Powodzenia !
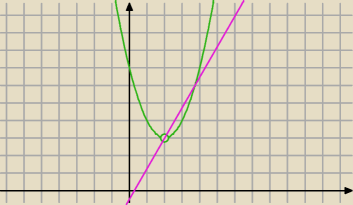 przez wierzchołek paraboli poprowadź prostą o współczynniku kierunkowym a=√3
...dalej sam/sama
przez wierzchołek paraboli poprowadź prostą o współczynniku kierunkowym a=√3
...dalej sam/sama 
 parabola
y=x2 − 4x + 7
wiemy, ze jeden z wierzcholkow trojkata to wierzcholek paraboli, zatem policzmy wierzcholek
paraboli.
parabola
y=x2 − 4x + 7
wiemy, ze jeden z wierzcholkow trojkata to wierzcholek paraboli, zatem policzmy wierzcholek
paraboli.