macierz
gosia: wyznacz rząd macierzy
1 0 4
A=1 2 1
1 3 1 wszystkie liczby do2
25 lis 19:36
Jack:
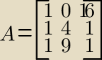
skoro wszystkie liczby do kwadratu , to to tak wyglada?
25 lis 20:49
gosia: Wgl nie ogarniam macierzy , ale na proste myslenie to tak myslałam też.
25 lis 21:12
gosia: rzad macierzy
1*4*1 + 0*1*1+1*9*16−16*4*1+0*1*1+1*9*1= 4+0+144−64+0+9=148−73=75
25 lis 21:14
gosia: Nie wiem tylko czy to poprawnie?
25 lis 21:14
'Leszek: Rzad macierzy to maksymalna ilosc liniowo niezaleznych wierszy
lub kolumn.
Rzad mozna obliczy za pomoca minorow czyli podwyznacznikow,
czyli oblicz wyznacznik tej macierzy ,jezeli bedzie≠0 ,to rzad wynosi 3,
jezeli bedzie rowny 0 , to skreslasz dowolny wiersz i dowolna kolumne
to bedzie wlasnie minor i tu widac ,ze jest ≠0.
25 lis 21:20
gosia: a wyznacznik liczymy jak ?
25 lis 21:23
'Leszek: Tak jak to zrobilas dobrze o godz 21.14 , czli rzad tej macierzy wynosi 3
25 lis 21:25
Janek191:
Powinno być
det = 1*4*1 + 0*1*1 + 1*9*16 − 16*4*1 − 0*1*1 − 1*9*1 = 144 − 73 = 71
25 lis 21:29
gosia: ok. .
A jak się rozwiazuje równanie macierzowe ?
np
| 4 −1| | −2 3|
x | 2 −2| = | −3 6|
?
25 lis 21:33
jc: Rząd macierzy = wymiar przestrzeni rozpiętej przez kolumny macierzy
Kolejne macierze mają ten sam rząd.
1 0 16
1 4 1
1 9 1
1 0 15
1 4 0
1 9 0
1 0 1
1 4 0
1 9 0
0 0 1
1 4 0
1 9 0
0 0 1
1 0 0
1 5 0
0 0 1
1 0 0
0 1 0
rząd = 3
25 lis 21:33
Jack:
X * A = B
X = B * A−1
odwroc macierz
[4 − 1]
[2 − 2]
25 lis 21:35
gosia: a czemu tam dalej masz same "−" ?
25 lis 21:35
gosia: a jak sie odwraca ?
25 lis 21:44
Jack: mozesz to zrobic na kilka sposobow
1. metoda przeksztalcen elementarnych
2. metoda dopelnien algebraicznych
ktore mialas na cwiczeniach?
za pewne to pierwsze...
zatem jak masz macierz
[4 −1]
[2 −2]
to dopisujemy do niej macierz jednostkowa
[4 −1|1 0]
[2 −2|0 1]
i przeksztalcamy tak dlugo az po lewej stronie znaku | uzyskamy macierz jednostkowa, a po
prawej jakas inna macierz.
25 lis 21:49
gosia: Jack , mam pytanie , bo wyżej 21:29 Janek napisał coś, i zastanawiam się dlaczego napisał "−"
od połowy do końca ?
25 lis 21:51
Jack:
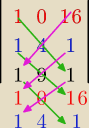
na przejsciu zielonym dodajemy, na rozowym odejmujemy
zatem najpierw zielone
1*4*1 + 1 * 9 * 16 + 1 * 0 * 1
teraz rozowe je odejmujemy zatem mozna dac minus przed nawias i w nawiasie bedzie wtedy plus
− (16*4*1 + 1*9*1 + 1*0*1)
wyznacznik to
1*4*1 + 1 * 9 * 16 + 1 * 0 * 1 − (16*4*1 + 1*9*1 + 1*0*1)
zatem po opuszczeniu nawiasu
1*4*1 + 1 * 9 * 16 + 1 * 0 * 1 − 16*4*1 − 1*9*1 − 1*0*1
25 lis 21:56
25 lis 21:58
gosia: Jack, a ta druga metoda?
25 lis 22:16
Jack: post 21:56 to wyznacznik macierzy 3x3
nie ma prostszej

a te 2 metody to mowilem odnosnie macierzy odwrotnej. (21:49)
25 lis 22:19
gosia: Tak , zrozumiałam , że mowa do macierzy odwrotnej.
25 lis 22:27
25 lis 22:28
gosia: Ale chyba nie bardzo wiem nadal jak zastosować te dwie metody przy odwroceniu...

25 lis 22:29
Jack:
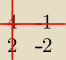
to jest metoda dopelnien algebraicznych, ktora sie oplaca ale maxymalnie do macierzy 3x3,
wiekszych juz nie.
polega ona na tym aby najpierw :
1) policzyc wyznacznik macierzy ktora chcemy obrocic
2) zbudowac macierz dopelnien algebraicznych
wzor jest taki
gdzie |A| to wyznacznik
A
D to macierz dopeplnien, a T oznacza ze jeszcze transponowana (zamiana miejscami kolum z
wierszai)
zatem zacznijmy, mamy macierz
[4 −1]
[2 −2]
wyznacznik tej macierzy to 4*(−2) − (−1)*2 = −8 + 2 = − 6
teraz budujemy macierz dopelnien, o co chodzi ?
patrzymy najpierw na liczbe "4" czyli lewy gorny rog macierzy.
robimy "wykreslenie" poziome i pionowe tam gdzie jest czworka i zostaje nam (−2)
(patrz rysunek)
i my patrzymy na wyznacznik z (−2), wyznacznik z −2 mozna zapisac jako |−2|
teraz dla −1 wykreslamy i zostaje nam 2, a patrzymy na wyznacznik czyli |2|
potem dla 2 mamy |−1| i dla |−2| mamy 4
budujemy macierz
[|−2| |2|]
[|1| |4|]
teraz zasada jest taka ze na glownej przekatnej dajemy plusy, a wszedzie indziej dopisuje
minusy czyli mam
[|−2| −|2|]
[−|1| |4|]
wyznacznik z liczby = ta liczba, zatem wyznacznik |−2| = − 2 itd, zatem otrzymuje macierz
[−2 −2]
[−1 4]
teraz ja transponujemy
[−2 − 1]
[−2 4]
no i macierz odwrotna to
A
−1 = [−2 −1]
25 lis 22:43
Jack:
lepiej to wymnozyc te −1/6
jak sie mnozy macierz przez liczbe ? otoz mnozymy kazdy element macierzy przez te liczbe.
zatem mielismy −1/6 razy macierz
[−2 −1]
[−2 4]
po wymnozeniu mamu
i teraz zeby rozwiazac tamto rownanie to musisz ta macierz pomnozyc przez macierz B
a dokladniej macierz B razy ta (bo kolejnosc mnozenia w macierzach ma znaczenie !)
25 lis 22:47
gosia: 
dziękuję, biorę się za przekalkulowanie tego co napisałeś

26 lis 11:55
26 lis 12:02
gosia: ok zmieniając liczby inny przyklad ale o to samo chodzi:(czy dobrze zrozumiałam)
[3 −2] [−1 2]
x [5 −4] = [−5 6]
wyznacznik to:
3*(−4)−(−2*5)= −12−(−10)= −12+10= −2
budujemy macierz dopełnień:
[ |−4| |5| ]
[ |−2| |3| ] czyli macierz nasza to
[−4 5 ]
[−2 3 ]
teraz transportujemy :
[−4 −2]
[ 5 3].
| | 1 | |
A−1 = − |
| * [−4 −2] = [2 1] |
| | 2 | |
26 lis 13:02
gosia: rozwiazując równanie wychodzi:
[−1 2] [2 1] =
[−7 −4]
[−25 −14] ?
26 lis 13:06
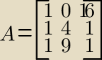 skoro wszystkie liczby do kwadratu , to to tak wyglada?
skoro wszystkie liczby do kwadratu , to to tak wyglada?
 na przejsciu zielonym dodajemy, na rozowym odejmujemy
zatem najpierw zielone
1*4*1 + 1 * 9 * 16 + 1 * 0 * 1
teraz rozowe je odejmujemy zatem mozna dac minus przed nawias i w nawiasie bedzie wtedy plus
− (16*4*1 + 1*9*1 + 1*0*1)
wyznacznik to
1*4*1 + 1 * 9 * 16 + 1 * 0 * 1 − (16*4*1 + 1*9*1 + 1*0*1)
zatem po opuszczeniu nawiasu
1*4*1 + 1 * 9 * 16 + 1 * 0 * 1 − 16*4*1 − 1*9*1 − 1*0*1
na przejsciu zielonym dodajemy, na rozowym odejmujemy
zatem najpierw zielone
1*4*1 + 1 * 9 * 16 + 1 * 0 * 1
teraz rozowe je odejmujemy zatem mozna dac minus przed nawias i w nawiasie bedzie wtedy plus
− (16*4*1 + 1*9*1 + 1*0*1)
wyznacznik to
1*4*1 + 1 * 9 * 16 + 1 * 0 * 1 − (16*4*1 + 1*9*1 + 1*0*1)
zatem po opuszczeniu nawiasu
1*4*1 + 1 * 9 * 16 + 1 * 0 * 1 − 16*4*1 − 1*9*1 − 1*0*1
 a te 2 metody to mowilem odnosnie macierzy odwrotnej. (21:49)
a te 2 metody to mowilem odnosnie macierzy odwrotnej. (21:49)

 to jest metoda dopelnien algebraicznych, ktora sie oplaca ale maxymalnie do macierzy 3x3,
wiekszych juz nie.
polega ona na tym aby najpierw :
1) policzyc wyznacznik macierzy ktora chcemy obrocic
2) zbudowac macierz dopelnien algebraicznych
wzor jest taki
to jest metoda dopelnien algebraicznych, ktora sie oplaca ale maxymalnie do macierzy 3x3,
wiekszych juz nie.
polega ona na tym aby najpierw :
1) policzyc wyznacznik macierzy ktora chcemy obrocic
2) zbudowac macierz dopelnien algebraicznych
wzor jest taki
 dziękuję, biorę się za przekalkulowanie tego co napisałeś
dziękuję, biorę się za przekalkulowanie tego co napisałeś 