Proste i okrąg - geometria analityczna
Gal:
Napisz równanie kierunkowe stycznych do danego okręgu o i równoległych do prostej k, jeśli:
o: (x−2)
2+(y−1)
2=4 k: y=2x
Wiem, że:
r=2
Współrzędne S to S(2,1)
W jaki sposób mogę to rozwiązać?
24 lis 23:18
Gal: (rysunek sam zrobiłem, mam nadzieję, że poprawnie)
24 lis 23:19
Eta:
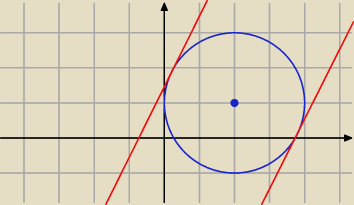
styczne mają równania:
y=2x+2√5−3 ,
y=2x−2√5−3
24 lis 23:26
Eta:
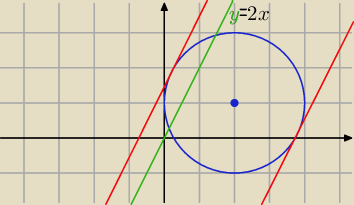
24 lis 23:30
Gal: Dzięki, ale jak to obliczyć?

24 lis 23:31
Jolanta: styczne mają takie samo a=2 y=2x+b
2x−y+C=0
teraz wzor na odległość prostej od punktu(środka w tym zadaniu)
d=U{|Ax0+By0+C|}{√a2+B2=r
24 lis 23:34
jc: Np. możesz poszukać b takiego, że prosta y=2x+b przecina okrąg
w dokładnie jednym punkcie (równanie kwadratowe ma 1 rozwiązanie, Δ=0).
24 lis 23:34
Eta:
k: y=2x s∥ k to s: y=2x+b ⇒ s: 2x−y+b=0
S(2,1) , r=2
odległość d środka S od stycznej jest równa r =2
| | 2*2−1*1+b| | |
d= |
| = 2 ⇒ |b+3|=2√5⇒ b1=... lub b2=.... |
| | √22+(−1)2 | |
podstaw za b
1 i b
2
otrzymasz dwie styczne : y= 2x+b
1 v y= 2x+b
2
24 lis 23:36
24 lis 23:37
jc: y=2x+b
(x−2)2+(y−1)2=4
(x−2)2+(2x+b−1)2=4
5x2−(8−4b)x+(b−1)2=0
Δ = 4*4(2−b)2−4*5(b−1)2=0
4−2b=√5(b−1), b=−3+2√5
lub
4−2b=−√5(b−1), b=...
24 lis 23:59
 Napisz równanie kierunkowe stycznych do danego okręgu o i równoległych do prostej k, jeśli:
o: (x−2)2+(y−1)2=4 k: y=2x
Wiem, że:
r=2
Współrzędne S to S(2,1)
W jaki sposób mogę to rozwiązać?
Napisz równanie kierunkowe stycznych do danego okręgu o i równoległych do prostej k, jeśli:
o: (x−2)2+(y−1)2=4 k: y=2x
Wiem, że:
r=2
Współrzędne S to S(2,1)
W jaki sposób mogę to rozwiązać?
 styczne mają równania:
y=2x+2√5−3 , y=2x−2√5−3
styczne mają równania:
y=2x+2√5−3 , y=2x−2√5−3

