Geometria analityczna Maturzysta : Witam, proszę uprzejmie o wyjaśnienie mi tego zadania. Nie ukrywam iż geometria analityczna nie jest moja mocna strona. W trójkącie rownoramiennym abc gdzie ac=BC podstawa zawiera się w prostej p: 3x−7y+35=0 natomiast ramię BC w prostej z: 5x−2y−19=0. Wyznaczyć równanie prostej w której jest zawarty bok ac jeżeli punkt p(−2,0) należy do boku ac.

Mila:

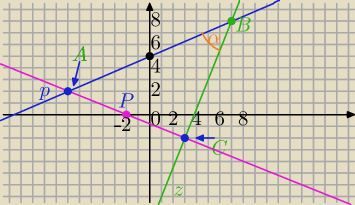
	3
p: 3x−7y+35=0 y=		x+5 punkty wykresu (0,5) ,(7,8)
	7

	5		19
z: 5x−2y−19=0 , y=		x−
	2		2

AB− podstawa Kąty ostre przy przy podstawie są równe. Prosta AC: m: y=ax+b i (−2,0) ∊M⇔ −2a+b=0, b=2a m: y=ax+2a Kąt między prostymi p i z:

	|a2−a1|
tgα=
	1+a1*a2

	5   3   − 2   7
tgα=
	5   3   1+ *   2   7

	35−6
tgα=		=1
	14+15

Kąt między prostymi p i m

	3   | −a|   7
1=		i Wsp. kierunkowy AC <0
	3   |1+ *a|   7

	3		3		3		3
1+		a=		−a lub 1+		a=a−
	7		7		7		7

	2		5
a=−		lub a=		( to prosta || do z)
	5		2

	2		4
m: y=−		x−		równanie kierunkowe
	5		5

⇔ m: 2x+5y+4=0 równanie ogólne. Możesz sprawdzić czy |AC|=|BC|

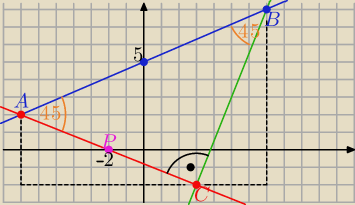
Eta: Podobnie ...... tgα=.... =1 ⇒ α= 45^o to trójkąt ABC jest prostokątny i równoramienny więc proste BC ⊥AC

	5		2
ich współczynniki kierunkowe : aBC=		, aAC=−		i P(−2,0)∊AC
	2		5

	2
prosta AC : y=−		(x+2) / *5
	5

AC: 2x+5y+4=0