Oblicz Przsemo: 2cos(2x)≥−1 Może mi ktoś pomóc zrobić to zadanie krok po kroku bo nie jestem pewien rozwiązania.

Jack: dzielac obustronnie przez 2

	1
cos(2x) ≥ −
	2

podstawiajac t = 2x

	1
cos(t) ≥ −
	2

gdy znajdziemy przedzial dla t, to dla x tez bez problemu znajdziemy

Przsemo: To jeszcze rozumiem ale wynik mi wychodzi od −⁵₁₂ do ⁵₁₂ więc trochę kiepsko. Gdzieś robię błąd ale nie wiem gdzie:(

PW:

	1
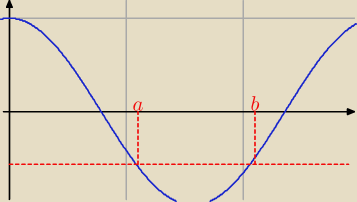
Rysujesz wykres cos(u) dla u∊<0, 2π) i czerwoną przerywaną linię y = −		. Nie nadają się
	2

tylko te x, które są zawarte między a i b.

	1		1
Jeżeli wiesz, dla jakiego a jest cosa = −		i dla jakiego b jest cosb = −		, to
	2		2

zadanie rozwiązane (widoczne przedziały przesuwamy o wielokrotność okresu).

Przsemo: Już odkryłem błąd ^π₂ odejmowałem ^π₃. Wynik to będzie <−^π₃+kπ ; ^π₃+kπ> zgadza się?

Jack:

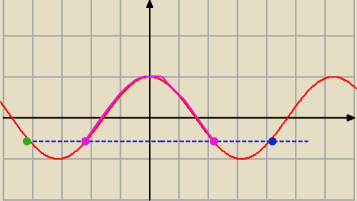
	1
cosinus przyjmuje wartosc −		dla :
	2

(180−60) oraz (180+60) czyli dla 120 oraz 240 stopni,

	2		4
czyli		π oraz dla		π
	3		3

zatem

	1
cos(t) ≥ −
	2

	2		2
t ∊ <−		π + 2kπ;		π + 2kπ>
	3		3

zatem

	2		2
t ≥ −		π + 2kπ i t ≤		π + 2kπ
	3		3

	2		2
2x ≥ −		π + 2kπ i 2x ≤		π + 2kπ
	3		3

wyznacz x...

PW: Nie rozumiem. Jeżeli chcesz korzystać z pomocy, to nawiązuj dialog ze mną, a nie ze sobą.

PW: To nie do Ciebie, Jack. Twój wybór przedziału jest nawet lepszy, bo jedna seria rozwiązań i nie trzeba nic tłumaczyć..

Przsemo: Dziękuję. PW bardziej od rozwiązania chciałem znaleźć miejsce w którym robię notorycznie błąd, teraz znalazłem więc już raczej nie będę go powielał.Jeszcze raz dzięki, robicie świetną robotę.

PW: