Geometria analityczna Behemot: Na płaszczyźnie dany jest punkt A= (8 4), . Prosta AB jest nachylona do osi OX pod kątem a = ° 60 . Wyznacz współrzędne punktu B, wiedząc, że AB = 22. Pomoże ktoś? Zadanko z wczorajszej próbnej rozszerzonej.

PW: Prosta ma równanie y = ax + b, współczynnik kierunkowy jest równy tangensowi kąta nachylenia: a = tg60° a = √3. Prosta ma równanie y = √3x + b; współczynnik b obliczymy podstawiając współrzędne punktu A: 4 = √3^.8 + b b = 4 − 8 √3 = 4(1 − 2√3). Równanie prostej: (1) y = √3x + 4(1 − 2√3). Współrzędne szukanego punktu B spełniają więc układ równań (1) i (2): (2) (x−8)² + (y−4)² = 22² (kwadrat odległości |AB|). Nie liczę, bo pewnie już gdzieś jest policzone.

PW: Jak na poziom rozszerzony, to pomyślmy tak: − Po przesunięciu o wektor [−8, −4] otrzymamy punkt A' = (0, 0). Prosta po przesunięciu nadal jest pochylona do osi OX pod tym samym kątem 60 (obrazem prostej w przesunięciu jest prosta do niej równoległa). Prosta ma więc równanie (1) y' = √3x' , szukamy na niej punktu B' odległego od (0,0) o 22. Rozwiązujemy układ równań (1) i (2): (2) x'² + y'² = 22². Jest to łatwiejsze rachunkowo niż w poprzedniej wersji. Po znalezieniu punktu B' przesuwamy go o wektor przeciwny dostając szukany punkt B, i zadanie rozwiązane dość szybko.

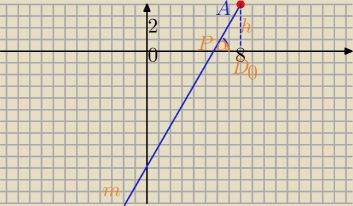
Mila: |AB|=22,α=60^o tg60^o=√3 y=√3*x+b 4=8√3+b b=4−8√3 Prosta : m: y=√3x+4−8√3 Teraz można rozwiązać układ równań : (x−8)²+(y−4)²=22² i y=√3x+4−8√3 otrzymamy dwa punkty przecięcia Tu rachunki niezbyt przyjazne. ================= Łatwiej będzie tak:

	22√3
H=		=11√3 to będzie wysokość trójkąta BAD ( o kątach 60,30,90)
	2

h=4 Punkt przecięcia : y=√3x+4−8√3 i y=4−11√3 punkt na prostej poniżej OX √3x+4−8√3=4−11√3⇔√3x=−3√11 x=−3 B₁=(−3,4−11√3) Lub Punkt przecięcia : y=√3x+4−8√3 i y=4+11√3 punkt na prostej powyżej OX √3x+4−8√3=4+11√3 √3x=19√3 x=19 B₂=(19,4+11√3) ===========

Eta: A(8,4) AB: y= √3(x−8)+4 ⇒ AB: y=√3x+4−8√3 B∊ AB to B(x, √3x+4−8√3) i |AB|²= 22² zatem: (x−8)²+(√3x−8√3)²= 22² (x−8)²+ 3(x−8)²=22² ⇒ 4(x−8)²=22² ⇒ |x−8|=11 ⇒ x=19 v x= −3 to y= 19√3+4−8√3= 4+11√3 lub y= −3√3+4−8√3= 4−11√3 B( .....,....) lub B(....., ....)

Mila: Nie taki diabeł straszny jak go malują.

Eta:

Mila: Jakoś maturzyści nie mają problemu z rozszerzoną maturą. W zeszłym roku było inaczej.

PW: Może zbledli i boją się pytać?

Lipa: nie rozumiem tego momentu (x−8)²+(y−4)²=22² nie ma nic mowy o jakimkolwiek okregu.

PW: Po prostu wbili cyrkiel w A i szukają naokoło w odległości 22 (czyli rysują okrąg; tam gdzie przetnie się z prostą są szukane dwa punkty B₁ i B₂.

Lipa: dzieki za pomoc