| 1 | ||
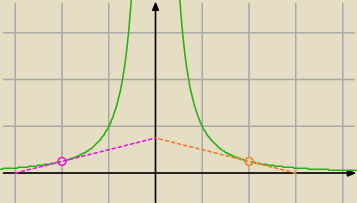
W ktorym punkcie wykresu funkcji f(x)= | , gdzie x≠0 nalezy poprowadzic styczna do tego | |
| x2 |
| 9 | ||
wykresu, aby pole trojkata ograniczonego ta styczna i osiami wspolrzednych bylo rowne | . | |
| 8 |
| −2x | −2 | |||
f'(x)= | = | |||
| x4 | x3 |
| −2 | ||
skad wiemy, ze a= |  | |
| x3 |
| 1 | ||
zauważ, że styczna do wykresu f(x)= | odkłada odpowiednio na 0x odcinek a | |
| x2 |
| ab | 9 | 9 | ||||
wiesz, że | = | ⇒ ab= | ||||
| 2 | 8 | 4 |
| b | ||
a jednocześnie | =tgα=f'(xp) i licz  | |
| a |
| 9 | ||
ab= | ||
| 4 |
| 9 | ||
b= | ||
| 4a |
| 9 | 1 | 9 | ||||||||||
= | * | = | |||||||||||
| a | 4a | a | 4a2 |
| 9 | |
=tgα=f'(xp) | |
| 4a2 |
| −2 | ||
f'(xp)= | ||
| xp3 |
| 9 | −2 | ||
= | |||
| 4a2 | xp3 |