Ekstrema XYZ:

	1		2
Wielomian określony wzorem w(x)=		x4+		x3
	4		3

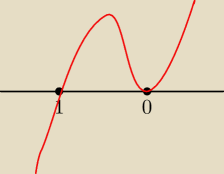
A) Nie ma ekstrema lokalnego B) Ma jedno ekstremum lokalne C) Ma dwa ekstrema lokalne D) Ma trzy ekstrema lokalne w'(x)=x³+2x²=x²(x+2) w(x) jest funkcja malejącą dla x∊(−∞;−1> w(x) jest funkcja rosnąca dla x∊<−1,+∞) ⇒ funkcja w(x) posiada jedno ekstremum lokalne, odp B Dobrze jest rozwiazane to zadanie?

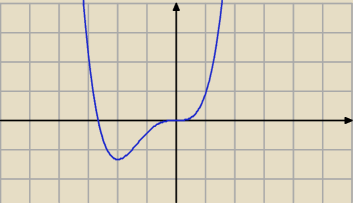
Janek191: f maleje w ( −∞ , − 2) , rośnie w ( − 2, +∞) Ma jedno ekstremum − minimum.