zad
Sanders:
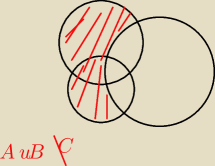
Jakie
zależności
zachodzą
między
zbiorami
ABC
gdy
zachodzi
równość
(A u B) \ C = (A\C) u B
Narysowalem je. Widzę, inne obszary zakreskowane na dwoch rysunkach.
Co one nam mówią?
23 lis 18:33
Sanders:
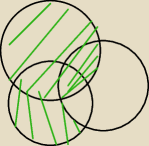
(A\C) u B
23 lis 18:34
===:
diagram dolny źle narysowałeś
23 lis 18:40
Sanders: Chodzi o to, że nie podpisałem który okrąg to który zbiór?
23 lis 18:42
===:
pokaż A\C
23 lis 18:44
Sanders:
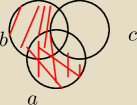
(A u B) \ C
23 lis 18:46
Sanders: Racja, poprawiam
23 lis 18:47
Sanders:
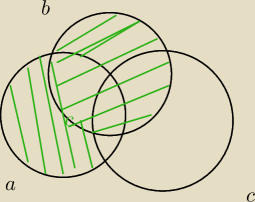
(A u B) \ C
23 lis 18:49
Sanders: No i porównuje sobie oba zbiory, i otrzymuje takie coś:
23 lis 18:49
Sanders: Żeby zachodziło P, to w L musi być B n C = zbiór pusty, tak?
23 lis 18:50
Sanders: zbiór z godziny 18:46, jest teraź źle narysowany

. proszę odwoływać się do zbioru czerwonego
z 18:33
23 lis 18:52
===:
dalej źle

Narysuj tylko A\C
23 lis 18:52
23 lis 18:53
23 lis 19:00
Sanders: teraz dobrze?
23 lis 19:00
===:
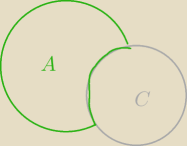
i "nałóż" teraz ∪B
23 lis 19:00
Sanders: ===? jaki wniosek z rysunku można wyciągnąć?
23 lis 19:02
===:
Przeczytaj treść zadania ... jaka zależność ma zachodzić między poszczególnymi zbiorami aby
zachodziła podana równość (czy nie widzisz, że niektóre muszą być rozłączne? )

23 lis 19:06
Sanders: aaa juz rozumiem, równość , mam zrobić tak, aby L = P, czyli
23 lis 19:07
Sanders: tak jak mówisz, niektóre zbiory muszą być rozłączne
23 lis 19:07
Sanders: nie mających wspólnego elementu
czyli BnC = zbior pusty
23 lis 19:08
===:
zaćmienie?

23 lis 19:08
Sanders: BnC = zbior pusty , tak"?
23 lis 19:08
===:
bingo

23 lis 19:08
Sanders: Mam jeszcze taki przykład
(AuB) \ (BnC) = AnC
23 lis 19:09
Sanders: Czy L lepiej jakoś rozpisać, bo tak mi ciężko je narysować
23 lis 19:10
===:
nie zauważyłem Twego postu z 18:50
23 lis 19:11
Sanders: domyśliłem się, bo ja to u siebie na kartce narysowałem, a tutaj ciężko mi było przerysować
używając dostępnych narzędzi, ale nic nie szkodzi
23 lis 19:11
Sanders: Jak narysować, że (AuB) że te elementy należą do zbioru, a te nie (BnC)
23 lis 19:16
Sanders: a nie chwilka, chyba sobie poradze
23 lis 19:16
23 lis 19:31
Sanders: jakiś pomyśl? może inaczej da się to zilustrować?
23 lis 19:34
Sanders: chyba nikt nie pomoze ze zbiorami
23 lis 19:56
===:
wykonaj działania

23 lis 20:00
Sanders: L = (A u B) n (BnC)' = (B' nA) u (AnC]) u (BnB') u (BnC')
23 lis 20:04
Sanders: BnB' da nam zbior pusty
23 lis 20:04
Sanders: (B' nA) u (AnC') u (BnC')
23 lis 20:04
Sanders: i co dalej
23 lis 20:04
Sanders:
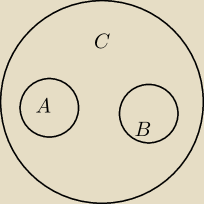
wykładowca nam podesłał położenie tych zbiorów do tego przykładu, dlaczego takie?
23 lis 20:09
Sanders: Nie wiem, czy się nie pomylił przpadkiem
23 lis 20:09
Sanders: wracając do zadania BnC' = musi byc pusty ,jesli chcemy AnC
23 lis 20:10
Sanders: ii

dalej

23 lis 20:13
Sanders: === − poszedłeś już spać

23 lis 20:17
Sanders: skoro coś nie należy do dopełnienia czegoś to należy do tego czegoś, no tak to rozumieim
23 lis 20:18
Sanders: Janek151 zerkniesz?
23 lis 20:49
Sanders: No trudno, jestem na razie zdany na siebie. Trzeba się mocno wziąć do roboty
23 lis 21:00
Eta:
Nie znam treści zadania ! Napisz jeszcze raz
23 lis 21:00
Sanders: ok jużpisze
23 lis 21:02
Sanders: Jakie zależności zachodzą między zbiorami ABC gdy równość (AuB) \ (BnC) = AnC
23 lis 21:02
Sanders: Jakie zależności zachodzą między zbiorami A B C gdy zachodzi równość (AuB) \ (BnC) = AnC
23 lis 21:03
23 lis 21:04
Sanders: muszę otrzymać L=P, dając jakieś założenia
23 lis 21:04
Sanders: i narysować położenie tych zbiorów
23 lis 21:04
Sanders: Jeśli masz chwilkę, to zastanów się nad tym zadaniem, jeśli nie, to sam spróbuje późnym
rankiem.
23 lis 21:05
Eta:
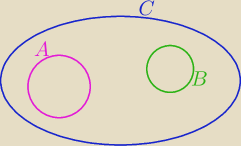
Tylko dla takich zbiorów zachodzi taka równość:
A⊂C i B⊂ C i A∩B=∅
bo (AUB)= obydwa kółka małe
B∩C= B
L=(AUB) \ (B∩C)= A i P= A∩C=A
L=P
zatem taka równość zachodzi
23 lis 21:09
Eta:
Te położenia zbiorów ,które podałeś w linku nie spełniają takiej równości
23 lis 21:11
Sanders: Tak, ale jak do tego doszłaś?
23 lis 21:12
Sanders: To co napisałaś jest jak najbardziej sensowne i w ogóle dobrze napisane, ale ja nie rozumiem
Twojej drogi dedukcji
23 lis 21:12
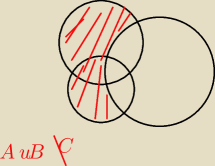 Jakie
zależności
zachodzą
między
zbiorami
ABC
gdy
zachodzi
równość
(A u B) \ C = (A\C) u B
Narysowalem je. Widzę, inne obszary zakreskowane na dwoch rysunkach.
Co one nam mówią?
Jakie
zależności
zachodzą
między
zbiorami
ABC
gdy
zachodzi
równość
(A u B) \ C = (A\C) u B
Narysowalem je. Widzę, inne obszary zakreskowane na dwoch rysunkach.
Co one nam mówią?
 (A\C) u B
(A\C) u B
 (A u B) \ C
(A u B) \ C
 (A u B) \ C
(A u B) \ C
 . proszę odwoływać się do zbioru czerwonego
z 18:33
. proszę odwoływać się do zbioru czerwonego
z 18:33
 Narysuj tylko A\C
Narysuj tylko A\C





 i "nałóż" teraz ∪B
i "nałóż" teraz ∪B




 wykładowca nam podesłał położenie tych zbiorów do tego przykładu, dlaczego takie?
wykładowca nam podesłał położenie tych zbiorów do tego przykładu, dlaczego takie?
 dalej
dalej

 Tylko dla takich zbiorów zachodzi taka równość:
A⊂C i B⊂ C i A∩B=∅
bo (AUB)= obydwa kółka małe
B∩C= B
L=(AUB) \ (B∩C)= A i P= A∩C=A
L=P
zatem taka równość zachodzi
Tylko dla takich zbiorów zachodzi taka równość:
A⊂C i B⊂ C i A∩B=∅
bo (AUB)= obydwa kółka małe
B∩C= B
L=(AUB) \ (B∩C)= A i P= A∩C=A
L=P
zatem taka równość zachodzi