Geometria analityczna
MAGDA : Wyznacz rownanie prostej zawierajacej wysokosc trojkata ABC poprowadzona z wierzcholka C mając
dane:
A=(−4,1) B=(0,5) C=(2,−2)
Prosiłabym jeszcze o rysunek do tego zadania
23 lis 14:41
===:
... a do zeszytu nie trzeba od razu wpisać?

23 lis 15:57
===:
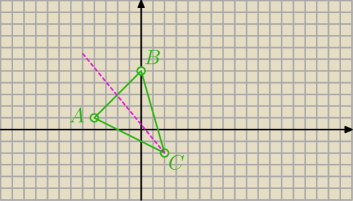
23 lis 16:01
===:
współczynnik kierunkowy prostej przechodzącej przez A i B
Prosta prostopadła do niej ma współczynnik a
2=−1
Równanie tej prostej to y+2=−1(x−2) ⇒ y=−x
23 lis 16:05
===:
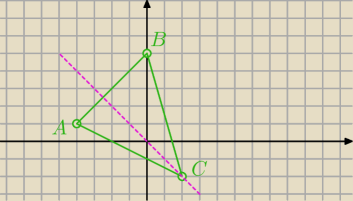
dokładniejszy rysunek
23 lis 16:08
poszukujący: 1) Równanie prostej AB:
y=ax+b.
AB: y=x+5
2) Niech H będzie spodkiem wysokości opuszczonej z wierzchołka C na bok AB.
Równanie prostej CH (czyli szukanej prostej):
y=mx+n.
Proste AB i CH są prostopadłe wtedy i tylko wtedy, gdy iloczyn ich współczynników kierunkowych
(liczb stojących przy x w równaniach prostych) jest równy −1.
Współczynnik kierunkowy prostej AB to 1, a prostej CH to m.
1*m=−1
m=−1
CH: y=−x+n
Prosta CH przechodzi przez punkt C=(2,−2).
−2=−2+n
n=0
CH:
y=−x
23 lis 16:09


 dokładniejszy rysunek
dokładniejszy rysunek