Oblicz granicę fasolus: Ktoś ma jakiś pomysł ? Oblicz granicę:

	e3x −1
lim
	sin9x

(x−−>0)

Jerzy:

	3e3x		3
= lim		= [		] = 3
	9cosx		1

Jerzy:

	3		1
Oj... =		=
	9		3

fasolus: mozna prosic o rozwiazanie krok po kroku skad sie to wzielo ?

Jerzy: Skorzystałem z reguły de l'Hospitala.

fasolus: Wykładowca niestety prosił, aby rozwiązać to bez uzywania powyzszej reguły

Mila: granice specjalne:

	ex−1
limx→0		=1
	x

	sinx
limx→0		=1
	x

===========

	e3x−1		9x		1		1		1
limx→0		*		*		=1*1*		=
	3x		sin(9x)		3		3		3

Mariusz:

	ex−1
limx→0
	x

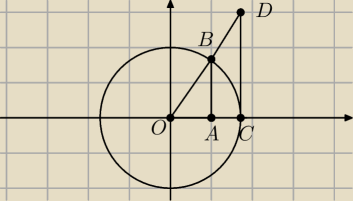
Rozpatrzyć granice jednostronne

	1		1
Wykazać równość limx→−∞(1+		)x=limx→∞(1+		)x
	x		x

	1
Zastosować podstawienie ex−1=
	z

	sinx
limx→0
	x

Korzystając z parzystości możemy ograniczyć się do policzenia tylko granicy prawostronnej Nierówności do trzech ciągów możemy wziąć w ten sposób Sprawdzamy pola trójkątów oraz wycinka kołowego widoczne na rysunku Granice które podała Mila występują przy liczeniu pochodnych pierwsza przy liczeniu pochodnych funkcji wykładniczych druga przy liczeniu pochodnych funkcji trygonometrycznych