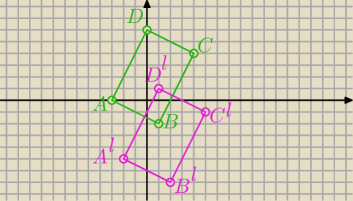
przesunięcie o wektor ax+b: Prostokąt o wierzchołkach A=(−3, 0), B=(1, −2), C=(4, 4), D=(0, 6) przesunięto o wektor v=[1. −5] Oblicz pole części wspólnej

Janek191: Znajdź punkty wspólne i oblicz pole otrzymanego prostokąta.

ax+b: Tyle to oczywiście i ja wiem. Ale jak to zrobić wykorzystując wektory

ax+b: wiesz jak to zrobić na wektorach

Mila: A=(−3, 0), B=(1, −2), C=(4, 4), D=(0, 6) AB^→=[4,−2] A'D'^→=[3,6] wektory prostopadłe Prosta AB: 3(x+3)+6*(y−0)=0 3x+6y+9=0 /:3 x+2y+3=0 Prosta A'D': A'=(−2,−5) 4*(x+2)−2*(y+5)=0⇔4x+8−2y−10=0 2x−y−1=0 Punkt przecięcia prostych P(x,y)

	1		7
2x−y−1=0 i x+2y+3=0⇔x=−		i y=−
	5		5

Masz 3 wierzchołki prostokąta;

	1		7
P(−		,−		),B i D'− liczysz pole tego trójkąta i mnożysz przez 2.
	5		5

ax+b: serdeczne dzięki za próbę pomocy. Ale to nie o taki sposób chodzi.

Kacper: To jak lepiej wiesz , to po co pytasz ?

ax+b: gdybym wiedział to nie pytałbym. A ciebie to już na pewno nie ma o co pytać.

Mila: Musisz sprecyzować czego oczekujesz. Masz napisane równania prostych (wektory wykorzystane) i rozwiązanie jest prawidłowe.

PW: Wektor D'B ma długość .... Wektor DB ma długość ... Prostokąty są podobne, więc stosunek pól jest równy kwadratowi skali podobieństwa (stosunku

	D'B
		).
	DB

Nie liczę szczegółów, bo może znowu nie będzie się podobać.

ax+b: Bardzo sprytnie ... dzięki

ax+b: tylko czy oby na pewno te prostokąty są podobne (duży i część wspólna) ?

PW: Nie sprawdziłem. Jeżeli nie są, to pomysł do niczego.

Puma: Juz to Bardzo sprytnie gdzies czytalem czy to nie aby czarny Krzysiek