Ekstrema funkcji oraz [unkty przegięcia
Ola: Znaleść ekstrema funkcji oraz punkty przegięcia :
22 lis 19:08
Jack:
no, to, jak to sie robi?

zacznijmy od dziedziny funkcji oraz pochodnej i dziedziny pochodnej

22 lis 19:25
Ola: Wlaśnie wgl mi to nie wychodzi ;C
22 lis 19:28
Jack: no to pokaaaa

Dziedzina = ?
pochodna = ?
22 lis 19:28
Ola: Niby mam :
x1=1
x2=−1
22 lis 19:29
Ola: ale punk przegięcia mi nie wychodzi
22 lis 19:29
Jack:
D
f = R \ {0}
szukamy ekstremow :
y' = 0
x
4 − 1 = 0
(x
2−1)(x
2+1) = 0
x = − 1 lub x = 1
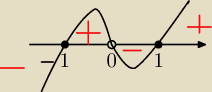
rysujemy krzywa i mamy :
minimum w −1
minimum w 1
to byly ekstrema, co do punktu przegiecia −> dalszy post
22 lis 19:39
Jack:
w poprzednim poscie mielismy
w celu znalezienia punktu przegiecia potrzebna nam druga pochodna
| | − 6x2 | | 6 | |
y'' = 2 − |
| = 2 + |
| |
| | x6 | | x4 | |
teraz przyrownujemy ja do zera.
y'' = 0
x
4 + 3 = 0
x
4 = − 3
otrzymujemy sprzecznosc ; o
zatem brak punktu przegiecia, no nic nie zrobimy.
22 lis 19:45
Ania: Dziękuję ślicznie wlasnie cos mi nie pasowało z tym punktem

Dziękuję

22 lis 19:47
Ola: Dziękuję

22 lis 19:47
Jack: Nie musisz zmieniac ciagle nicku

22 lis 19:47
 zacznijmy od dziedziny funkcji oraz pochodnej i dziedziny pochodnej
zacznijmy od dziedziny funkcji oraz pochodnej i dziedziny pochodnej 
 Dziedzina = ?
pochodna = ?
Dziedzina = ?
pochodna = ?
 Df = R \ {0}
Df = R \ {0}
 Dziękuję
Dziękuję 

