rozwiaz nierownosc
6.167 : 2sinπx/3≥√3
22 lis 18:38
zef:
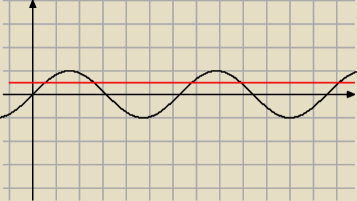
czyli:
Podstawiam:
| πx | | π | |
| ≥ |
| +2kπ ⇒ πx≥π+6kπ ⇔ x≥1+6k |
| 3 | | 3 | |
| πx | | 2π | |
| ≤ |
| +2kπ ⇒ πx≤2π+6kπ ⇔ x≤2+6k |
| 3 | | 3 | |
22 lis 18:43
6.167 : Dziekuje
22 lis 18:48
6.167 : a dlaczego t∊ do takiego przedzialu jak wgl wyznczac taki przedzial
22 lis 18:51
zef: | | √2 | | √3 | |
Tam wszędzie zamiast |
| ma być oczywiście |
| , rozwiązane jest dobrze ale źle |
| | 2 | | 2 | |
klikałem na klawiaturze

22 lis 18:53
6.167 : jasne tylko moje pytanie jest dlaczego t raz jest wieksze a raz mniejsze a nie tylko wieksze
jak ?
22 lis 18:54
zef: Wiem że okres sinusa to 2π
i że jest dodatni w 1 i 2 ćwiartce
| | π | | π | | 2π | |
sinus przyjmuje wartość √3{2} dla x= |
| oraz π− |
| = |
| |
| | 3 | | 3 | | 3 | |
22 lis 18:54
zef: Popatrz na rysunek

22 lis 18:55
6.167 : tak ja wiem ze w 1 i 2 z wierszyka i umiem wyznaczyc sinx=√3 tylko nierozumiem dlavczego
musze dac ze t raz jest ≥ a raz ≤ dziekuje za pomoc
22 lis 18:58
zef:
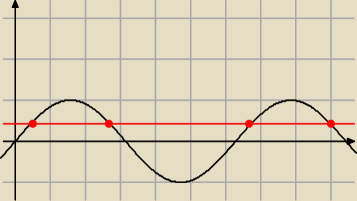
| | √3 | |
Bo musisz sprawdzić przedział kiedy ten sinus jest większy od |
| |
| | 2 | |
22 lis 19:01



