Jednokładność Radek: Prosta l2 jest obrazem prostej l1: x+2y−4=0 w jednokładności o środku w punkcie P(2,−1) i skali k=−2. Podaj równanie prostej l2. Gdzie jest błąd?

	1
l1: y = 2 −		x
	2

	1
S ∊ l1, S (x, 2 −		x), S' (x', y')
	2

→ → PS' = k * PS

	1
[x' − 2, y' + 1] = −2[x − 2, 2 −		x + 1]
	2

[x' − 2, y' + 1] = [−2x + 4, −6 + x] x' − 2 = −2x + 4 x' = −2x + 6 y' + 1 = −6 + x y' = x − 7 (to się nie zgadza)

Kacper: kontynuując...

	x'
x'=−2x+6 ⇒ x=3−
	2

	x'		x'
y'=x−7=3−		−7=−		−4
	2		2

	x
y=−		−4
	2

Radek: dzięki, czyli jednak nie ma błędu

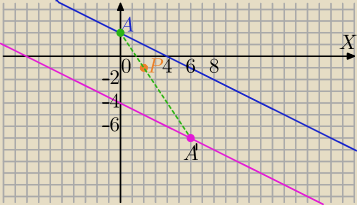Mila: l1: x+2y−4=0 Obrazem prostej w jednokładności jest prosta równoległa⇔ l₂: x+2y+C=0 Wystarczy znaleźć obraz jednego punktu należącego do prostej l₁ A=(0, 2)∊l₁ P=(2,−1) A'=(x,y) PA'^→=k*PA^→⇔ [x−2,y+1]=−2*[0−2,2+1] [x−2,y+1]=[4,−6] x−2=4 i y+1=−6 A'=(6, −7) Podstawiamy do równania l₂: x+2y+C=0 6+2*(−7)+C=0 6−14+C=0 ⇔C=8 l₂: x+2y+8=0 ===========