Zilustrowanie zbioru wszystkich punktów płaszczyzny szatek: Jak narysować zbiór rozwiązań na płaszczyźnie? |x−4|+|3y|=6 Podzieliłem w zależności na ćwiartki i wyszło

	1		10
1 ćw.: y= −		+
	3		3

	1		2
2 ćw.: y=		+
	3		3

	1		2
3 ćw.: y= −		−
	3		3

	1		10
4 ćw.: y=		−
	3		3

Jak teraz narysować wykres tego?

Kacper: A gdzie x?

szatek:

	1		1
no x zgubiłem przy tych		i −		ale już ogarnąłem co i jak
	3		3

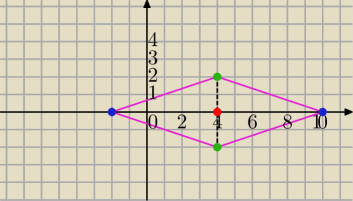Mila: To będzie romb. S=(4,0)− punkt przecięcia przekątnych |x−4|+|3y|=6 1) dla y=0 mamy : |x−4|=6⇔x−4=6 lub x−4=−6 x=10 lub x=−2 2) x=4 |3y|=6 y=2 lub y=−2 II sposób

	1
|y|=−		|x−4|+2⇔
	3

	1
y=−		|x−4|+2 dla y≥0 (I i II ćw.)
	3

lub

	1
y=		|x−4|−2 (III i IV ćw.)
	3