Pilne dżela: Dany jest czworościan foremny o wysokości H i krawędzi długości a. a) Wykaż, że 3H²=2a² b) Wiedząc dodatkowo, że wysokość jest o 1 krótsza od krawędzi, oblicz a. Wynik przedstaw w postaci a+b√c, gdzie a,b, c należy do N

Kacper: Pilne bo na jutro ?

dżela: tak

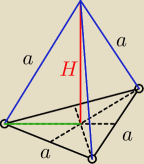
Jack: grunt to dobry rysunek

	2
ten zielony fragment to nic innego jak		wysokosci podstawy (gdyz mamy w podstawie
	3

trojkat rownoboczny a w takim trojkacie od srodka tego trojkata do dowolnego wierzcholka to odleglosc wynosi 2/3h − wiemy to chociazby z okregu opisanego na trojkacie rownobocznym)

	a√3
wysokosc rownobocznego to
	2

	2		2		a√3		a√3
zatem		tej wysokosci to		*		=
	3		3		2		3

no i teraz z pitagorasa

	a√3
H2 + to zielone czyli (		)2 = a2
	3

	3a2
H2 +		= a2 /*9
	9

9H² + 3a² = 9a² 9H² = 6a² /:3 3H² = 2a² czyli to co nalezalo udowodnic.

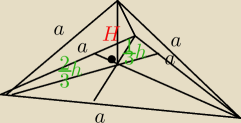
agulka: 1.3H²=2a²

	a√3		3a2
h=		, h2=
	2		4

Z tw. Pitagorasa:

	2
H2+(		*h)2=a2
	3

	4
H2=a2−		*h2
	9

	4		3a2
H2=a2−		*
	9		4

	a2
H2=a2−		/*3
	3

3H²=3a²−a² 3H²=2a²