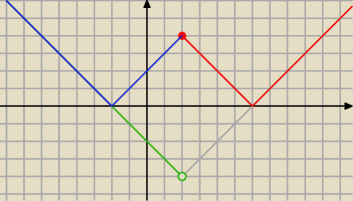
 wiec tak, nasza funkcja to
f(x) = ||x−2|−4|
wartosc bezwzgledna(ta na czerwono) oznacza odbicie tego co jest ponizej osi OX nad os.
zatem funkcje |x−2| − 4 odbije nad os, wiec rozpatrzmy jak sie ona zachowuje.
nazwijmy ja pomocniczo g(x) = |x−2| − 4
dla x ≥ 2
g(x) = x−2 − 4 = x − 6 (narysuje to na szaro − wraz z odbiciem juz na czerwono)
dla x < 2
g(x) = 2−x − 4 = − x − 2 (to na zielono, a z odbiciem juz niebieskie)
no to narysujmy wykres (nie zapominajac ze f(x) to odbicie tej czesci g(x) ktora jst ponizej
osi OX).
Koncowy wykres to fragment niebiesko−czerwony
teraz odczytaj dla jakiego igreka (u ciebie m) bedzie miec 3 rozwiazania dodatnie (tzn. dla x>0
szukamy 3 igrekow dodatnich)
i jak znajdziesz takie to podstawiasz ze to jest 7−5m.
i rozwiazujesz.
wiec tak, nasza funkcja to
f(x) = ||x−2|−4|
wartosc bezwzgledna(ta na czerwono) oznacza odbicie tego co jest ponizej osi OX nad os.
zatem funkcje |x−2| − 4 odbije nad os, wiec rozpatrzmy jak sie ona zachowuje.
nazwijmy ja pomocniczo g(x) = |x−2| − 4
dla x ≥ 2
g(x) = x−2 − 4 = x − 6 (narysuje to na szaro − wraz z odbiciem juz na czerwono)
dla x < 2
g(x) = 2−x − 4 = − x − 2 (to na zielono, a z odbiciem juz niebieskie)
no to narysujmy wykres (nie zapominajac ze f(x) to odbicie tej czesci g(x) ktora jst ponizej
osi OX).
Koncowy wykres to fragment niebiesko−czerwony
teraz odczytaj dla jakiego igreka (u ciebie m) bedzie miec 3 rozwiazania dodatnie (tzn. dla x>0
szukamy 3 igrekow dodatnich)
i jak znajdziesz takie to podstawiasz ze to jest 7−5m.
i rozwiazujesz.
| 3 | ||
m < 1 i m > | ||
| 5 |
| 3 | ||
m ∊ ( | ; 1) | |
| 5 |