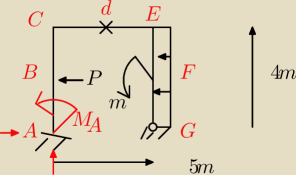
x dzoan: Witam chcialam sie zapytac o ∑Ma=0 czy jest ok −Ma−120−480=0 czyli Ma=600? gdzie P=40kn i moment M=40knm sa srodku belki

dzoan: Ha=280kN? Va=0? Ma=600knm?

dzoan: lub Ma=720?

dzoan: ?

yht: punkt G to utwierdzenie ? jeśli tak, to wg mnie powinno być: −Ma−P*2m−m−Rgy*5m−Mg = 0 jeśli punkt G jest zwykłą podporą nieprzesuwną, to −Ma−P*2m−m−Rgy*5m = 0 co ma oznaczać ten x przy d ?

dzoan: to nie wazne na razie

dzoan: co to Mg

yht: to moment utwierdzenia. On pojawi się tylko wtedy, gdy G jest utwierdzeniem

dzoan: do obliczen i tak usuwam ta podpore poprawej

dzoan: nie mialam czegos takiego

dzoan: czyli ma=−420?

dzoan: −Ma−P*2−M−q*4m*5m?

yht: jak dla mnie −q*4m*2m zamiast −q*4m*5m

dzoan: Bo na odcinku E−G jest obciazenie q=60kn/m

dzoan: ok

dzoan: czyli yszlo git −600

yht: nie uwzględniając tej podpory G wychodzi Ma = −600

dzoan: Dobra to zamieniam zwrot momentu Ma i teraz mam pytanie bo obliczam rownanie momentow w kazdym z przedziałow i czy jest git A−C 0<x<2 M(0)=600knm M(2)=40knm A−C 2<x<4 M(0)=40knm M(4)=120knm

dzoan: C−E 0<x<5 M(0)=M(5)=120knm E−G 0<x<2 M(0)=120knm M(2)=520knm G−F2<x<4 M(2)=880 M(4)=powinno byc chyba 0 a wychodzi jakis cyrk

dzoan: moze rozpisze chodzi mi szczegolnie o ta ostatnia belke E−F 0<x<2 M(x)=(Ha−P)x−q*x*^x₂+120 przedział E−G 2<x<4 M(x)=(Ha−P)x−q*x*^x₂+520−M?

yht: wydaje mi się że (Ha−P)x jest źle bo Ha i P są w różnych odległościach

dzoan: a nie beda po tej samej dlugosci i tak? czyli w domysle 5?

dzoan: zreszta to tutaj nie ma znaczenia chyba?

yht: Gdyby (Ha) i (P) były pionowe to wtedy by tak było jak piszesz ale zauważ że dla punktu F moment od siły P będzie 0 zaś dla punktu A moment będzie równy Ha*2m

dzoan: racja

dzoan: a wczesniejsze przedziały do A−E jest ok?

yht: ja niestety muszę zmykać może ktoś inny pomoże.. ew. jeszcze zerknę dziś wieczorkiem na ten temat

yht: wydaje mi się że A−E jest źle bo np. w A−C momenty będą się sumować Ma = 600 działa w tę samą stronę co moment od Ha więc (jak dla mnie) w A−C będzie M(2) = 600+280*2 = 1160

dzoan: Brales pod uwage jak cos ze zmienilam zwrot momentu Ma?

relaa: Punkt G z rysunku wynika, że jest to utwierdzenie z przegubem, a co za tym idzie jest to podpora nieprzesuwna. Jeżeli w punkcie G nic nie ma to M_A = 600kNm, a R_A = 280kN. Liczymy momenty. ∑ M_B = 600kNm − 280kN • 2m = 40kNm ∑ M_C = 600kNm − 280kN • 4m + 40kN • 2m = −440kNm Na odcinku C − E nie działa żadna siła, czy moment, więc nic nam się nie zmienia zatem moment jest tam stały i wynosi −440kNm. Liczymy moment w punkcie F z prawej strony

	kN
∑ MPF = −60		• 2m • 1m = −120kNm, więc z lewej będzie powiększony o moment M
	m

	kN
∑ MLF = −60		• 2m • 1m + 40kNm = −80kNm,
	m

dla upewnienia policzmy inaczej

	kN
∑ MLF = 600kNm − 280kN • 2m − 60		• 2m • 1m = −80kNm
	m

	kN
∑ MPF = 600kNm − 280kN • 2m − 60		• 2m • 1m − 40kNm = −120kNm.
	m

relaa: Oczywiście zamiast R_A winno być H_A.

dzoan: dzięki wielkie

relaa: Proszę. Wytrzymałość materiałów, czy jakiś inny przedmiot?

dzoan: tak

dzoan: a w punkcie G nie bedzie 600−60*4*2−40−40*2?

relaa: W takim razie życzę powodzenia w nauce i zrozumieniu go, ponieważ jest on podstawowym przedmiotem z którego inne korzystają, bez niego nie zrozumiesz kolejnych.

relaa: Przecież w punkcie G nic nie ma (nie trzeba nic liczyć), więc moment wynosi 0, ale jeżeli tego nie widzisz to licz, lepsze to niż nic.