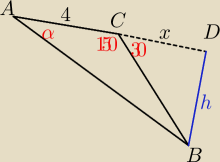
Trójkąt Piotr: W trójkącie rozwartokątnym ABC dane są: [AC] = 4, kąt ACB = 150 stopni oraz tg α = 1/3. Oblicz długość wysokości trójkąta ABC poprowadzonej z wierzchołka B.

	x√3
Wiem, że h=
	3

	1		x√3/3
Zatem		=		? Jeżeli tak, to x=x√3−4, jak mogę obliczyć h?
	3		x+4

Janek191:

	h		1
tg α =		=
	4 + x		3

	h		√3		√3
tg 30o =		=		⇒ h = x*
	x		3		3

więc

	√3   x *   3		1
		=
	4 + x		3

x √3 = x + 4 x*( √3 − 1) = 4

	4
x =
	√3 − 1

=============

	1
h =		*(4 + x)
	3

Wstaw za x i oblicz h

Piotr: dzięki, łatwo się zamieszać w tym zadaniu więc dużo mi pomogłeś

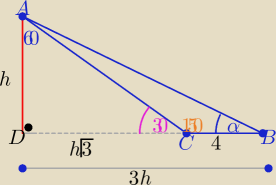Eta: W takich zadaniach : porządny rysunek .... to 3/4 sukcesu !

	1		h
tgα=		=
	3		3h

	2
zatem 3h= h√3+4⇒ h(3−√3)=4 /* (3+√3) ⇒ 6h= 4(3+√3 ⇒ h=		*(3+√3)
	3