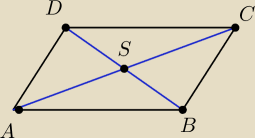
Dowód wektorowy Adrian: Udowodnij wektorowo, że punkt przecięcia przekątnych równoległoboku dzieli je na połowy. Bardzo proszę o rozwiązanie od początku do końca, zadanie było kilkakrotnie wpisywane, jednak pozostawione bez konkretnej odpowiedzi (zapewne jest łatwe, próbowałem, ale nic mądrego nie wyszło). Dzięki z góry.

lol: 0 = (DC + BA) = (DS+SC) + (BS+SA) = (DS+BS) + (SC+SA) Skoro suma dwóch wektorów nierównoległych wynosi 0 to oba te wektory muszą być zerowe. Zatem DS = SB i AS =SC

jc: lol, przecież te równości zachodzą dla dowolnego punktu S. A=(0,0), B=(3,0), C=(3,3), D=(0,3), S=(1,2) Wszystkie równości z pierwszej linii zachodzą, a jednak DS=(1,−1), SB=(2,−1), AS=(1,2), SC=(2,1).

jc:

	1		1
Dowód: B − A = C − D. Stąd		(A+C)=		(B+D), co oznacza, że środek
	2		2

odcinka AC jest środkiem odcinka BD.