romby: W rombie ABCD, punkt E dzieli bok AB, o długości a w stosunku 2:3 licząc od wierzchołka A. Odległość punktu E od przekątnej AC jest 3 razy mniejsza od odległości punktu E od przekątnej BD. Wykaż, że pole tego rombu jest równe 4/5a².

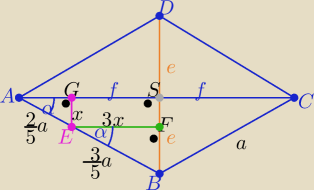
Eta: Z podobieństwa trójkątów AEG i BEF i ABS z cechy (kkk)

x		2		5		3		3x
	=		⇒ e=		x i		=		⇒ f=5x , x>0
e		5		2		5		f

z twierdzenia Pitagorasa w ΔABS :

	25		100		125
f2+e2=a2 ⇒ a2=		x2+		x2 ⇒ a2=		x2
	4		4		4

	4
to x2=		a2
	125

	1		5
Pole rombu : P=		*2f*2e ⇒ P=f*2e ⇒ P=5x*2*		x=25x2
	2		2

	4		4
to P= 25*		a2 ⇒ P=		a2
	125		5

c.n.w

romby: Dziękuję!

Eta: