
 A ja kocham planimetrię
A ja kocham planimetrię  Porządny rysunek to w zadaniach z planimetrii 3/4 sukcesu !
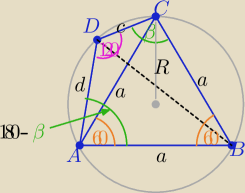
zad 1
Z warunku wpisania czworokąta w okrąg |∡ABC|= 180o−120o= 60o
zatem uwzględniając treść zadania : ΔABC jest równoboczny
P(ABCD)= P(ABC)+P(ADC)
Porządny rysunek to w zadaniach z planimetrii 3/4 sukcesu !
zad 1
Z warunku wpisania czworokąta w okrąg |∡ABC|= 180o−120o= 60o
zatem uwzględniając treść zadania : ΔABC jest równoboczny
P(ABCD)= P(ABC)+P(ADC)
| a√3 | ||
R=4 ⇒ | =4 ⇒ a=4√3 to P(ABC)= 12√3 | |
| 3 |
| 1 | d*c√3 | |||
Zajmijmy się teraz trójkątem ADC: P(ADC)= | *d*c*sin120o = | |||
| 2 | 4 |
| 1 | 1 | |||
P(ABD)= 2P(BCD) to | *a*d*sin(180o−β) = | *a*c*sinβ ⇒ d=2c | ||
| 2 | 2 |
| 48 | ||
48=7c2 ⇒ c2= | ||
| 7 |
| d*c√3 | c2√3 | 24√3 | ||||
P(ADC)= | = | = | ||||
| 4 | 2 | 7 |
| 24√3 | ||
zatem P(ABCD)= 12√3+ | = .................... | |
| 7 |
 zad2 też ciekawe ...... z małym "haczykiem"
zad2 też ciekawe ...... z małym "haczykiem"  Może ktoś inny się skusi
Może ktoś inny się skusi  Jak nie ...to jutro podam rozwiązanie
Jak nie ...to jutro podam rozwiązanie
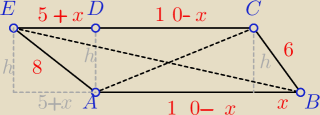 założenia :
h, x > 0 , 5+x > 0 −−−−> x > − 5
10−x>0 −−−> x < 10
z Pitagorasa
h2 = 82 − (5+x)2
h2 = 62 − x2
0 = 28 + x2 − (5+x)2 −−−−> (5+x)2 − x2 = 28
(5+x−x)(5+x+x) = 28 −−−−−> 5(5+2x) = 28 −−−−> 25 + 10x = 28
założenia :
h, x > 0 , 5+x > 0 −−−−> x > − 5
10−x>0 −−−> x < 10
z Pitagorasa
h2 = 82 − (5+x)2
h2 = 62 − x2
0 = 28 + x2 − (5+x)2 −−−−> (5+x)2 − x2 = 28
(5+x−x)(5+x+x) = 28 −−−−−> 5(5+2x) = 28 −−−−> 25 + 10x = 28
| 3 | ||
10x = 3 −−−−> x = | ||
| 10 |
| 9 | 9 | 3591 | ||||
czyli x2 = | oraz h2 = 36 − ( | ) = | ||||
| 100 | 100 | 100 |
| 3591 | 9 | 3591 | 991 | 4582 | ||||||
m2 = | + (10 − | ) = | + | = | ||||||
| 100 | 100 | 100 | 100 | 100 |
| √4582 | ||
m = | <−to ta krotsza przekatna | |
| 10 |
| 3 | 3591 | 22500 | 3591 | 26091 | ||||||
n2 = (15 + | )2 + | = | + | = | ||||||
| 10 | 100 | 100 | 100 | 100 |
| √26091 | ||
n = | ||
| 10 |
| √4582 | ||
m = | ||
| 10 |
| √26091 | ||
n = | ||
| 10 |
| 3 | ||
Niech x= | ||
| 10 |
| 3 | 3 | 100 | 3 | 97 | 97 | 9409 | ||||||||
m2=h2+(10− | )2, 10− | = | − | = | , ( | )2= | ||||||||
| 10 | 10 | 10 | 10 | 10 | 10 | 100 |
| 3591 | 9409 | 13000 | ||||
m2= | + | = | =130 | |||
| 100 | 100 | 100 |
| 3 | 3 | 150 | 3 | 153 | ||||||
n2=(15+ | )2+h2, 15+ | = | + | = | , | |||||
| 10 | 10 | 10 | 10 | 10 |
| 153 | 23409 | |||
( | )2= | |||
| 10 | 100 |
| 23409 | 3591 | 27000 | ||||
n2= | + | = | =270 | |||
| 100 | 100 | 100 |

