Problem z dziedziną oraz z przeciwdziedziną funkcji
OLa123: Witam , mam takie zadanie:
Dane są funkcje f(x)=x2 +3 , gdzie x∊R oraz g(x)=√x−1 , gdzie x∊ <1,∞) , znajdz złożenie
funkcji
f(g(x)) oraz g(f(x)) , a także określ i ich dziedzinę i przeciwdziedzinę.
Wszystko byłoby pięknie i ładnie bo złożenia bez problemu znajduję:
f(g(x))=x+2
g(f(x))=√x2 +2
ale nie potrafię określić ich dziedziny i przeciwdziedziny..nie rozumiem tego byłabym wdzięczna
jakby ktoś mi to wytłumaczył
skąd i jak ..po kolei.
20 lis 14:38
Puma:
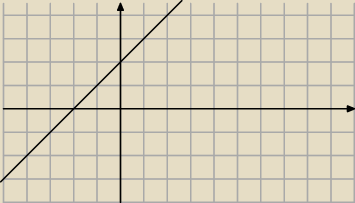
y=x+2
20 lis 14:43
Puma:
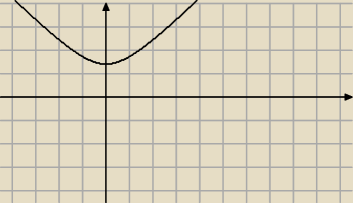
y=
√x2+2
20 lis 14:44
OLa123: no ok dziedziny już widze a co z przeciwdziedzinami?
20 lis 14:53
Puma: Weglug mnie dla 1 funkcji przeciwdziedzina to R
dla drugiej przeciedziedzina to <√2,∞)
20 lis 14:56
OLa123: z tą 1 to nie pasuje mi coś do końca....bo znalazłam u sb w zeszycie od <3,∞) ale skąd to się
bierze ...? a w 2 funkcji jak ja określiłaś?
20 lis 15:01
Puma: W drugiej to co pod pierwiastkiem bedzie zawsze dodatnie
czyli najmniejsza wartosc funkcji bedzie dla x=0 i y=√0+2= √2
20 lis 15:04
OLa123: a czasem dla 1 funkcji dziedzina to R a przeciwdziedzina to <0,∞) ?
20 lis 15:18
Puma: Kolega Jerzy zostal poproszony o pomoc tutaj moze sie odezwie .
20 lis 15:20
Jack: w czym problem?

20 lis 15:20
OLa123: tak jak w temacie , wydaję sie być banalnyxd ale mam problem z odszukaniem dziedziny i
przeciwdziedziny funkcji otrzymanych po złożeniu

20 lis 15:22
Puma: Jack
W okresleniu przeciwdzidziny zlozonej 1 funkcji .
20 lis 15:23
OLa123: ktoś coś ?

20 lis 15:39
Jack: hmm
ja to widze w ten sposob :
f(x)=x2 +3 Df = R, ZWf = <3;∞)
g(x)=√x−1 Dg = <1;∞) ZWg = <0;∞)
f(g(x)) = f(√x−1) = x−1+3 = x+2
Df(g(x)) = Dg = <1;∞) ZWf(g(x)) = ZWf = <3;∞)
g(f(x)) = g(x2+3) = √x2+3−1 = √x2+2
Dg(f(x)) = Df = R ZWg(f(x)) = ZWg = <0;∞)
20 lis 15:46
Jack: stop.
Cos namieszalem
20 lis 15:51
OLa123: co do 2 funkcji to przeciwdziedzina nie ma wynosić <√2 , +∞)?
20 lis 15:54
OLa123: dobra już widzę ....zrozumiałam ....przeciwdziedzina funckji 2 ma wynosić <√2 , +
∞)...reszta
się zgadza Jack

dziekuje Wam za pomoc

20 lis 16:02
Jack: tak, powinno byc <√2 ; ∞)
aczkolwiek cos nadal chyba mieszam ...
20 lis 16:07
 y=x+2
y=x+2
 y=√x2+2
y=√x2+2



 dziekuje Wam za pomoc
dziekuje Wam za pomoc 