równania liniowe z dwiema niewiadomymi
paweł : mam równanie |x|+x=y+|y|
jak do tego podejść czy rozpisać to na 4 przypadki?
pomocy
20 lis 13:04
Jerzy:
Masz to pewnie narysować na płaszczyźnie ?
20 lis 13:06
paweł : zgadza się
20 lis 13:06
Jerzy:
Rozpatruj oddzielnie 4 przypadki:
20 lis 13:07
paweł : rozpatruje x<0 y<0 , x≥0 y≥0 , x<0 y≥0 , x≥0 y<0
i wychodzi 0=0 , x=0, y=0, x=y
i to tyle? chyba że coś źle policzyłem
20 lis 13:23
Adamm:
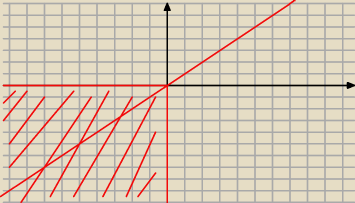
20 lis 13:33
Jerzy:
drugi i czwarty przypadek żle.
20 lis 13:33
paweł : w takim razie jak powinno to algebraicznie wyglądać?
20 lis 13:43
PW: Są cztery możliwości:
|x| + x = 0 lub |x| + x = 2x
|y| + y = 0 lub |y| + y = 2y,
są więc do rozwiązania cztery równania:
(1) 0 = 0
(równość spełniona dla wszystkich (x,y) w których x < 0 i y < 0 (rozwiązanie stanowią punkty
III ćwiartki).
(2) 0 = 2y
równość spełniona dla par (x, y), w których x < 0 i y = 0 (rozwiązaniami są punkty ujemnej
półosi OX)
(3) 2x = 0
równość spełniona dla (x, y), w których x ≥ 0 i y < 0 (rozwiązaniami są punkty o pierwszej
współrzędnej równej 0 i drugiej ujemnej, czyli ujemna półoś OY).
(4) 2x = 2y
równość spełniona dla par (x, y), w których x ≥ 0 i y ≥ 0 i x = y (punkty leżącej w I ćwiartce
półprostej o początku (0, 0) określonej równaniem y = x).
20 lis 13:44
Adamm: narysowałem ci, ujemna półoś y oraz x należy, wszystkie pary takie że x<0 oraz y<0, oraz
y=x
20 lis 13:44
paweł : dziękuję za wyjaśnienie

20 lis 13:47

