pilne! ewe7: Oblicz objętość ostrosłupa prawidłowego trójkątnego, wiedząc, że wysokość ściany bocznej ma długość 12dm i tworzy z wysokością ostrosłupa kąt 30⁰.

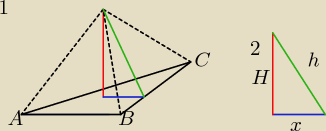
Cedro: RYSUNEK 1) czerwony −>Wysokość ostrosłupa zielony −> Wysokość ściany bocznej (12dm) niebieski −> ¹₃ Wysokości podstawy (trójkąt równoboczny) Kąt między ścianą czerwoną a zieloną wynosi 30 stopni ( treść zadania ) Tak więc korzystając z sinusa 30 stopni uzyskujemy : sin 30= ^x_h ¹₂ = ^x_12dm 2x = 12dm x = 6dm x = 60 cm Korzystamy z twierdzenia Pitagorasa aby obliczyć H ( Wysokość ostrosłupa ) tak więc : x²+ H² = h² 6²+H²=12² H²=12²−6² H²=144−36 H²=108 H=√108 H=6√3 Skoro x = 6 dm to wysokość podstawy wynosi 18 dm ( 3 * 6dm ) z właściwości trójkąta równobocznego wiemy że : h=^a√3₂ Tak więc : 18 = ^a√3₂ 36 = u{a√3} ³⁶_√3 = a a = 12√3 Pole podstawy − > Pp Pp = ¹₂*a*h Pp=¹₂*12√3*18 Pp=6√3*18 Pp=108√3 Objętość Ostrosłupa −> V V=Pp*H V=108√3*6√3 V=108*3*6 V=1944 dm²