Równanie z parametrem
Darek: Wyznacz wszystkie wartości parametru m, m ∈R, dla których pierwiastki równania
(m+1)x
2−3mx+4m=0 są liczbami rzeczywistymi i każdy z nich jest większy od 1.
Wiem, że Δ>0 i x
1, x
2>1 ale licząc Δ wychodzą bardzo dziwne liczby

20 lis 09:42
===:
Δ=9m2−16m2−16m
−m(7m+16)>0 i co tu dziwnego?
20 lis 10:08
===:
Pracuj nad dalszymi założeniami ... to co podajesz x
1*x
2 jest tu "ni pricziom"

20 lis 10:11
Darek: Później licząc x1 i x2 wychodzi x1=3m−√−7m2−16m2(m+1)
20 lis 10:12
===:
to nie jest Ci do niczego potrzebne i błędne

Zauważ, źe 0,9*5 też jest większe niżeli 1 ale x=0,9 nie spełnia założeń
20 lis 10:15
Darek: Nie chcę mnożyć x1*x2, napisałem x1 , x2>1 ( pomiędzy jest przecinek, jeśli dobrze
zrozumiałem i o to Ci chodzi)
20 lis 10:18
===:
1) Ustal przedział dla m wynikający z Δ
20 lis 10:21
===:
2) xw>1
20 lis 10:21
===:
3)

to już dla Ciebie

20 lis 10:22
20 lis 10:27
===:
iksowa współrzędna wierzchołka Twojej paraboli

20 lis 10:29
===:
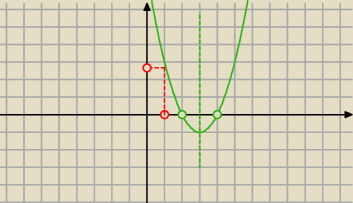
albo tak
20 lis 10:39
===:
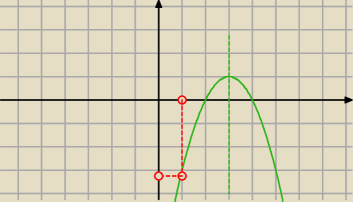
albo tak
20 lis 10:42
Darek: Ze wzoru p=−b2a ?
Wychodzi mi m∊(−∞,−1)∪(2,+∞)
I teraz muszę połączyć te dwa przedziały?
20 lis 10:46
===:
oczywiście

20 lis 10:53
===:
ale sprawdź raz jeszcze te wyliczenia dla p

20 lis 10:55
Darek: Czyli m∊(−167; −1) i to koniec zadania?
20 lis 10:55
===: przepraszam ... OK

20 lis 10:57
===:
to dopiero początek zadania .... patrz na moje rysunki

20 lis 10:57
Darek: Nie rozumiem co robić dalej
20 lis 11:02
===:
Parabola może "leżeć" jak na rysunku pierwszym lub drugim.
Zależy to od współczynnika a czyli
(m+1)x
2...
Czy musimy uwzględniać oba położenia

20 lis 11:07
Darek: W sensie a>0 ∨ a <0?
Podstawiając m>−1 ∨ m<−1
I kiedy to połączę z poprzednim przedziałem on się nie zmienia
20 lis 11:16
===:
z Δ i xw policzyłeś interesujący Cię przedział dla m
W tym przedziale a<0 zatem rysunek drugi
Z niego wynika trzeci warunek a mianowicie
f(1)<0 ... policz
20 lis 11:23
Darek: Dlaczego taki warunek?
20 lis 11:35
===:
dobrze Ci wychodzi ... to nie zmienia poprzedniego przedziału ...
a dlaczego warunek ... patrz na położenie paraboli

20 lis 11:41
Darek: Ok, rozumiem już

To już koniec zadania?
20 lis 11:45
===: tak

Zapamiętaj "ten mechanizm"

20 lis 11:46
Darek: Dzięki wielkie za pomoc

20 lis 11:47
Mateusz: a≠0
m+1≠0⇒m∊ℛ−{−1}
x1>1
x2>1
x1−1+x2−1>0
(x1−1)(x2−1)>0
x1+x2>2
x1x2−(x1+x2)>−1
I obliczasz ze wzorów Vietea
x1+x2=−b/a
x1x2=c/a
20 lis 12:00
PW: Tak się zastanawiam − czy dla
m = − 1 równanie przybierające postać
3x − 4 = 0
mające rozwiązanie
nie spełnia warunków zadania?
20 lis 14:20


 Zauważ, źe 0,9*5 też jest większe niżeli 1 ale x=0,9 nie spełnia założeń
Zauważ, źe 0,9*5 też jest większe niżeli 1 ale x=0,9 nie spełnia założeń
 to już dla Ciebie
to już dla Ciebie 

 albo tak
albo tak
 albo tak
albo tak






 To już koniec zadania?
To już koniec zadania?
 Zapamiętaj "ten mechanizm"
Zapamiętaj "ten mechanizm" 
