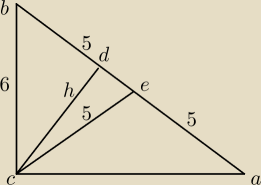
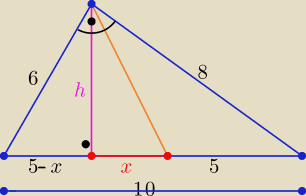
dobrze? Pati18773: Dany jest trójkąt prostokątny ABC o bokach długości 6, 8, 10. Odcinek CD jest jego wysokością, a E środkiem boku AB (zobacz na rysunku). Oblicz długość odcinka DE. Szukana: IdeI=? h²=xy IabI=10 IdbI=x IadI=y=10−x h²=x(10−x) h=√x(10−x) (√x(10−x))²+x²=6² x(10−x) +x²=36 10x−x²+x²=36 x=3.6 h=3.6(10−3.6)=4.8 IdeI=y (4.8)²+y²=5² 23.04+y²=25 y²=1.96 y=1.4 IdeI=1.4

Saizou : jak już miałaś BD to DE=BE−BD DE=5−3.6=1.4

Pati18773: a no w sumie xd

Mila:

1		1
	*6*8=		*10*h
2		2

48=10h h=4.8 6²=4.8²+|BD|² |BD|²=6²−4,8²=(6−4.8)*(6+4.8) |BD|²=1.2*10.8=12.96 |BD|=3.6 |DE|=5−3.6

Eta:

	ab		6*8
h=		=		=4,8
	c		10

h²=(5−x)(5+x) ⇒ 25−x²=23,04 ⇒ x²=1,96 ⇒ x=1,4

Eta: i założenie x∊(0,5)