Równania stycznych
Majk: Napisz równania stycznych do wykresu funkcji f(x) = 2x2 − 5x + 1, przechodzących przez punkt
P(2; −3).
Wyznaczyłem z pochodnych jedną styczną o równaniu: y = 3x − 12, aczkolwiek nie wiem, czy jest
to jedyna styczna i jak wyznaczyć drugą (jeżeli istnieje).
19 lis 17:30
Puma:
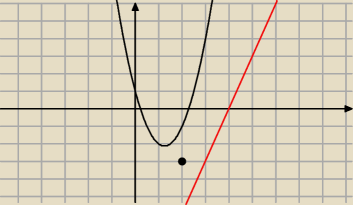
cos jednak nie tak
19 lis 17:33
Majk: 3x−9, pomyliłem się przy przepisywaniu
19 lis 17:34
Puma:
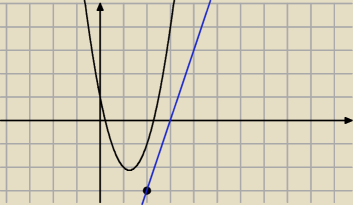
Ale dalej prosta nie jest styczna do wykresu sprawdz obliczenia
Widzisz ze jeszcze jedna musi byc
19 lis 17:38
Jack:
Styczna do wykresu przechodzaca przez P(2, −3).
Wykres funkcji to 2x2 − 5x + 1
Niech nasza styczna bedzie styczna do wykresu w punkcie (xo, f(xo))
czyli w punkcie (xo, 2xo2 − 5xo + 1)
wtedy wspolczynnik kierunkowy stycznej to pochodna w punkcie xo
zatem
f '(x) = 4x − 5
f '(xo) = 4xo − 5
zatem rownanie stycznej to : (korzystamy z rownania prostej czyli y = a(x−x1) + y1)
y = 4xo − 5(x − xo) + 2xo2 − 5xo + 1 = 4xo − 5x + 5xo + 2xo2 − 5xo + 1
y = −5x + 2xo2 + 4xo + 1
jednakze ta styczna przechodzi przez punkt (2, −3)
zatem podstawiamy wspolrzedne tego punktu
−3 = −5*2 + 2xo2 + 4xo + 1
7 = 2xo2 + 4xo + 1
2xo2 + 4xo − 6 = 0 /:2
xo2 + 2xo − 3 = 0
rozwiaz to rownanie i otrzymasz 2 takie proste.
19 lis 17:46
Eta:
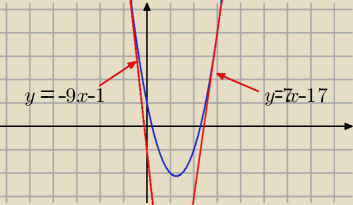
19 lis 18:14
Eta:
@Jack
równanie stycznej : y=(4xo−5)(x−xo)+2xo2−5xo+1 P(x,y) ⇒ x=2 y= −3
......................
xo2−2xo+3=0
19 lis 18:18
Jack: tak , faktycznie, pardon

20 lis 16:52
 cos jednak nie tak
cos jednak nie tak
 Ale dalej prosta nie jest styczna do wykresu sprawdz obliczenia
Widzisz ze jeszcze jedna musi byc
Ale dalej prosta nie jest styczna do wykresu sprawdz obliczenia
Widzisz ze jeszcze jedna musi byc

