:)
Metis: jc
Mogę prosić o twoją pomoc w jednym zadaniu z fizyki?
19 lis 15:08
jc: Co masz ciekawego?
19 lis 17:20
19 lis 17:47
19 lis 17:51
Jack:
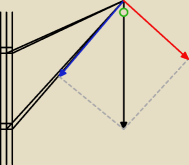
nie chcialbym przeszkadzac, ale nie trzeba tej sily rozlozyc na skladowe, np tak?
19 lis 18:05
Metis: Tak, ale nie pamiętam już tego z LO

19 lis 18:06
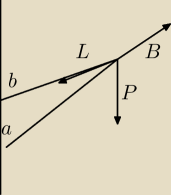
jc: Patrzymy na punkt końcowy belki.
L = wartość siły z jaką ciągnie lina.
B = wartość siły z jaką odpycha belka.
P = zaczepiony ciężar.
α = kąt pomiędzy pionem a liną (liczony tak, jak dla belki)
β = kąt pomiędzy pionem a belką (jak na rysunku)
Równowaga sił
L cos α = B cos β (siły poziome)
L sin α + P = B sin β (siły pionowe)
Rozwiązanie:
L (cos α sin β − sin α cos β) − P cos β = 0
L = P cos β / sin(β − α)
Podobnie znajdujesz B.
19 lis 18:13
jc: Może nie siły poziome/pionowe, tylko poziome/pionowe składowe sił.
19 lis 18:15
Metis:
A czy sformułowanie "siła działająca W ... " jest prawidłowe? Czy siła działająca NA
?
19 lis 18:17
jc: Ja bym powiedział: siły działające na punkt (w naszym zadaniu punkt na końcu belki).
19 lis 18:22
Metis: A do czego potrzebne mi B ?
L = P cos β / sin(β − α)
więc wszystko tutaj mamy podane
P=10kN
19 lis 18:28
Metis: Chyba, że źle patrzę.
19 lis 18:31
jc: Nie interesuje Cię siła z jaką ściskana jest belka? To jest właśnie B.
19 lis 18:36
Metis: Odpowiedzią będzie wypadkowa sił L i B?
19 lis 18:37
Metis: Możesz narysować mi poglądowy rysunek bo jakoś tego nie widzę.
19 lis 18:37
jc:
19 lis 18:41
jc: Zamień litery α, β!
19 lis 18:42
Metis: OK , korzystałem ze złego rysunku!

Dzięki Wielkie
jc, teraz rozumiem.
19 lis 18:44
Metis:
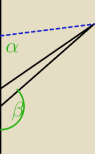
tylko jeszcze te kąty:
α= kąt pomiędzy pionem a liną (liczony tak, jak dla belki)
β = kąt pomiędzy pionem a belką (jak na rysunku)
zgadza się?
19 lis 18:53
jc:
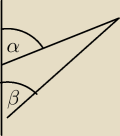
19 lis 18:59
Metis: Dzięki Wielkie

19 lis 19:00
Metis: Tylko co potem gdy obliczę i L i B ?
19 lis 19:05
Metis: Złożyć je metodą równoległoboku i obliczyć wypadkową?
19 lis 19:09
jc: Oj, pomyliłem trochę. Powinno być tak
L sin α = B sin β (siły poziome)
L cos α + P = B cos β (siły pionowe)
Wtedy
L sin(α − β) = P sin β
B sin(a − β) = P sin α
Ale sprawdź lepiej.
19 lis 19:13
jc: A co właściwie chcesz znaleźć?
19 lis 19:13
Metis: Obliczyć wartość siły działającej w pręcie

19 lis 19:14
jc: Czyli siłę, z jaką ściskana jest belka (pręt).
B = P sin α / sin(α − β)
Podstaw liczby i będziesz miał wynik.
19 lis 19:16
Metis:
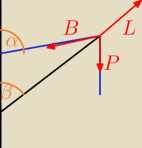
I rysunek wygląda tak:
19 lis 19:20
Metis: Wynik się zgadza

Dzięki!
19 lis 19:25
jc: Zamień na rysunku literę B z literą L.
19 lis 19:26
Metis: ok, mój błąd.
19 lis 19:27
Metis: A z jakiego prawa korzystamy układając te równania :
L sin α = B sin β (siły poziome)
L cos α + P = B cos β (siły pionowe)
19 lis 19:34
jc: Suma sił działających na koniec pręta = 0 (przecież nie przyspiesza).
Suma składowych poziomych = 0.
L sin α − B sin β = 0
Suma pionowych składowych = 0
L cos α − B cos β + P = 0
19 lis 19:45
Metis: To jasne, tylko nie widzę czemu możymy wektor L * sin α itd.
19 lis 19:48
jc: Nie wektor, tylko długość wektora.
19 lis 19:49
Metis: Długość wektora

19 lis 19:50
Metis: Możesz mi jc wyjaśnić jak zapisujesz równość tych sił?
Nie wiem skąd te iloczyn sinusów kątów i długości wektorów, nie widzę tego.
19 lis 20:04
jc: Narysuj w układzie współrzędnych wektory
(0, −P)
(−L sin α, − L cos α)
(B sin β, B cos β)
A potem przyrównaj sumę do zera.
19 lis 20:10
Metis: Jesteś za dobry
jc 
Dawno nie miałem do czynienia z wektorami i tego nie rozumiem.
Powtórze sobie wszystko i wtedy wróce do tego zadania.
19 lis 20:16
jc: Miałeś już liczby zespolone?
Miałeś postać trygonometryczną liczby zespolonej?
To jest dokładnie to samo.
W zadaniu trochę inaczej mierzymy kąty: od pionu, nie od poziomu.
Tak wyglądałoby to na płaszczyźnie zespolonej:
−iP
−L(sin α + i cos α)
B (sin β + i cos β)
19 lis 20:24
Metis: Miałem

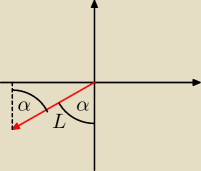
Ale nie wiem czemu długość tego wektora załóżmy L mnożymy razy sin kąta akurat α , nie widzę
trójkąta który rozpatrujemy.
19 lis 20:27
jc:
19 lis 20:31
 nie chcialbym przeszkadzac, ale nie trzeba tej sily rozlozyc na skladowe, np tak?
nie chcialbym przeszkadzac, ale nie trzeba tej sily rozlozyc na skladowe, np tak?


 Dzięki Wielkie jc, teraz rozumiem.
Dzięki Wielkie jc, teraz rozumiem.
 tylko jeszcze te kąty:
α= kąt pomiędzy pionem a liną (liczony tak, jak dla belki)
β = kąt pomiędzy pionem a belką (jak na rysunku)
zgadza się?
tylko jeszcze te kąty:
α= kąt pomiędzy pionem a liną (liczony tak, jak dla belki)
β = kąt pomiędzy pionem a belką (jak na rysunku)
zgadza się?



 I rysunek wygląda tak:
I rysunek wygląda tak:
 Dzięki!
Dzięki!

 Dawno nie miałem do czynienia z wektorami i tego nie rozumiem.
Powtórze sobie wszystko i wtedy wróce do tego zadania.
Dawno nie miałem do czynienia z wektorami i tego nie rozumiem.
Powtórze sobie wszystko i wtedy wróce do tego zadania.
 Ale nie wiem czemu długość tego wektora załóżmy L mnożymy razy sin kąta akurat α , nie widzę
trójkąta który rozpatrujemy.
Ale nie wiem czemu długość tego wektora załóżmy L mnożymy razy sin kąta akurat α , nie widzę
trójkąta który rozpatrujemy.
