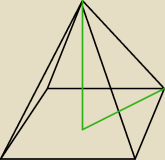
Krawędź podstawy ostrosłupa prawidłowego czworokątnego ma 14 cm długości,
a krawędź boczna tworzy z płaszczyzną podstawy kąt o mierze 60°.
Oblicz pole powierzchni i objętość tego ostrosłupa.
Czyli krawędź podstawy to 14.
Przekątna to 14√2 czyli podstawa ma trójkąt 7√2.
Czyli trójkąt o wymiarach 30,60,90.
To wysokość to 2a czyli 14√2
Przeciwprostokątna to a√3 czyli 7√6
Dobrze robię czy jednak coś źle?
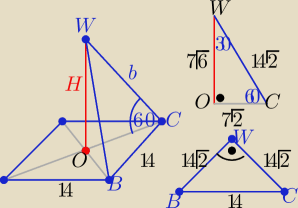Dobrze 
tylko te słowne komentarze są "pokrętnie" zapisane
" podstawa ma trójkąt " ...... co to za zapis?
H=7√6 , b=14√2
Ściany boczne są trójkątami prostokątnymi
| 1 | ||
V= | *142*7√6= .......... | |
| 3 |
| 1 | ||
Pc= 14%2+4* | *14√2*14√2=...... | |
| 2 |
| 5^2 | 52 |
| 2^{10} | 210 |
| a_2 | a2 |
| a_{25} | a25 |
| p{2} | √2 |
| p{81} | √81 |
| Kliknij po więcej przykładów | |
|---|---|
| Twój nick | |