Pomoc z rysunkiem do zadania.
Sonic: Punkty A(0,−5) oraz D(−3,−1) są kolejnymi wierzchołkami trapezu równoramiennego ABCD,
którego osią symetrii jest prosta o równaniu x+2y=0.
Oblicz współrzędne pozostałych wierzchołków oraz długość odcinka łączącego środki ramion tego
trapezu.
Mógłby mi ktoś pomóc z rysunkiem?
Zadanie wygląda na dość proste, tylko kompletnie nie wiem jak to rozrysować.
17 lis 23:11
Kacper:
Kłopot jest w narysowaniu układu i w nim prostej i dwoch punktów ?
17 lis 23:12
Puma:
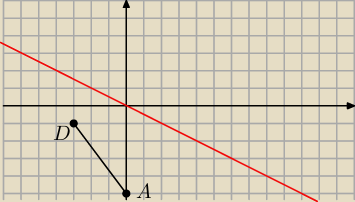
17 lis 23:21
Sonic: W zasadzie, to nie chciałem tego rozwiązywać w układzie.
Pytałem o czysty trapez i jak rozmieszczone są punkty. Chcę być pewny.

17 lis 23:21
Sonic: W układzie widzę zasada ta sama, liczę odległość punktu D od prostej,
następnie znajduję kolejny wierzchołek w takiej samej odległości po drugiej stronie prostej.
17 lis 23:23
Mila:
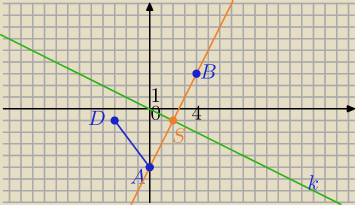
x+2y=0⇔
2y=−x
AD − ramię
AB⊥k
DC⊥k
AB:
y=2x+b i A∊prostej
−5=2*0+b, b=−5
y=2x−5
S− punkt przeciecia prostych
x=2, y=2*2−5=−1
S=(2,−1) − środek AB
B=(x,y)
B=(4,3)
próbuj dalej sam w taki sam sposób.
Prosta DC:
y=2x+b i D∊prostej
17 lis 23:23
Sonic: Dzięki wszystkim

17 lis 23:34


 x+2y=0⇔
2y=−x
x+2y=0⇔
2y=−x
