sinus PrzyszlyMakler: Dla jakich wartości parametru m równanie ma rozwiązania: sin ²x + sin x + m = 0 Pan Andrzej pisze: Równanie sin ²x + sin x + m = 0 ma rozwiązania wtedy i tylko wtedy gdy funkcja g(t)= t² + t + m określona w przedziale <−1;1> ma co najmniej jedno miejsce zerowe. Tu się zaczyna pierwsza kompletna niezrozumiałość dla mnie: Dlaczego ta funkcja musi być określona na tym przedziale? Przecież sinus musi przyjmować wartości z przedziału <−1;1> a nie być określony na przedziale <−1;1> Przejdźmy do rozwiązania:

	1
Równanie ma rozwiązanie gdy, 1) Δ=0 to wychodzi m =		<−− warunek jak najbardziej
	4

zrozumiały. Lub gdy delta jest większa od 0 [no bo wtedy ma dwa rozwiązania, prawda], ale jak nałożyć warunek na te rozwiązania? Pan Andrzej pisze, że f(1) ≥0 ale dla mnie to rzecz kompletnie niezrozumiała. A czy też nie powinniśmy sprawdzić, czy dla Δ=0 czyli m=1/4 sinx równanie wyjściowe osiąga wartości przedział€ <1;1> ? Jezu, wiem, że napisałem mase bzdur ale tak mi się to wszystko pomieszało, że potrzebuję, aby ktoś kto to bardzo dobrze rozumie wytłumaczył mi istotę tych warunków. Nie chcę rozwiązań, na internecie jest ich pełno, po prostu nie rozumiem

Jerzy: a) t = sin x , zatem t ∊ <−1,1>

PrzyszlyMakler: Dobra, trochę to sobie rozrysowałem i zrozumiałem, że w sumie na osi poziomej są 't' zamiast 'x', więc te 't' muszą być z przedział€ <1;1>, ale dalej nie rozumiem dlaczego f(1)≥0 i jak można narysować funkcję t² + t + m skoro nie znamy m

Jerzy:

	1
Dla Δ = 0 , mamy: t = −		a więc t ∊ <−1,1>
	2

Dla Δ > 0 , muszą być dodatkowo spełnione 3 warunki , aby t ∊ <−1,1>

	1
1) −1 < xw < 1 ( spełniony , bo xw = −
	2

2) f(−1) ≥ 0 3) f(1) ≥ 0

PrzyszlyMakler: Dlaczego 2) i 3)?

PrzyszlyMakler:

	1		1
a i odpowiedź jest <−2;		> a według Twojego warunku 2) byłoby <0;		>
	4		4

PrzyszlyMakler: bo f(−1)≥0 to 1 −1 + m ≥ 0 czyli m≥0 A odpowiedź ma od −2 do 1/4

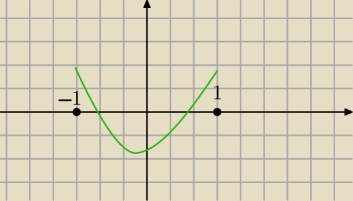
Jerzy: Widzisz dlaczego warunki 2 i 3 , aby rozwiązania należły do przedziału <−1,1> ?

PrzyszlyMakler: Widzę. Bo wtedy jest pewność, że się przetnie ta funkcja z osią OX, bo wiemy, gdy jest wierzchołek. Genialnie mnie naprowadziłeś na to, serio jestem mega wdzięczny tylko mi jeszcze wytłumacz dlaczego w odpowiedzi jest −2;1/4 a w Twojej od 0;1/4 PS. Już wykonałeś MEGA robotę bo W KOŃCU rozumiem skąd takie warunki. Tylko nie do końca jeszcze dlaczego f(−1) ≥0 i f(1)≥0, dlaczego nie na przykład f(−3/4)≥0 i f(1/100)≥0?

PrzyszlyMakler: bo wiemy gdzie jest wierzchołek*

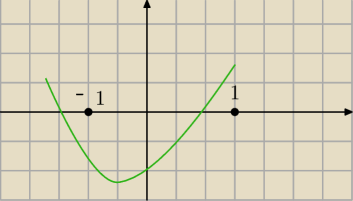
Jerzy: Nie jest spełniony warunek f(−1) ≥ 0 ( jedno miejsce zerowe wypada poza przedział <−1,1> )

PrzyszlyMakler: No tak, genialne. A co z odpowiedzią? Na innych forach z rozwiązaniami tego zadania, a także w rozwiązaniu Andrzeja pomijają warunek f(−1) ≥0

Jerzy: Podsumujmy:

	1
1) Δ ≥ 0 ⇔ m ≤
	4

2) f(−1) ≥ 0 ⇔ m ≥ 0 3) f(1) ≥ 0 ⇔ 2 + m ≥ 0 ⇔ m ≥ −2

	1
Część wspólna tych trzech warunków: m ∊ <−2,		>
	4

Jerzy:

	1
Bzdura... wychodzi : m ∊ <0,		> ..... jeszcze pomyslę
	4

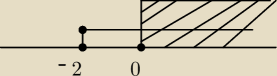
PrzyszlyMakler: Panie Jerzy− z warunku 2 mamy m≥0. Jak częścią wspólną warunków m≥0 ⋀ m≥−2 może być m≥−2

PrzyszlyMakler: @12:37 no dokładnie o tym mówię! PS. Napisałem post z 12:39 nim zobaczyłem ten 12:37

Jerzy: Podstawmy: m = −2 t² + t − 2 = 0 Δ = 9 √Δ = 3

	−1+3
t1 =		= 1
	2

	−1−3
t2 =		= −2
	2

sinx = −2 ( sprzeczność ) Moje rozwiązanie jest dobre , w książce jest pomyłka.

PrzyszlyMakler: Jak to? Przecież pytanie jest dla jakiego parametru m równanie marozwiązania dla m−2 ma jedno rozwiązanie. sinx = 1 (spełnia)

Jerzy: No faktycznie ... zasugerowałem się,że musi być jedno lub dwa rozwiązania. A więc:

	1
Skoro; xw = −		to faktycznie wrunek f(−1) ≥ 0 jest zbędny, bo warunek f(1) ≥ 0
	2

zapewnia nam zawsze co najmniej jedno rozwiąznie : t ≤ 1

PrzyszlyMakler: Okej. Dzięki Jerzy, że Ci się chciało. Czuję, że bardzo dużo mi to pomogło, normalnie prawie już płakałem, bo nie szło zrozumieć tego . Dziękuję raz jeszcze!

PW: Przekształćmy zadane równanie w sposób równoważny: (1) sin²x + sinx + m = 0

	1		1
sin2x + sinx + (		)2 − (		)2 + m = 0
	2		2

	1		1
(2) (sinx +		)2 =		− m.
	2		4

Warunkiem koniecznym istnienia rozwiązań jest

	1
(3)		− m ≥ 0.
	4

	1
Uwaga: nierówność nieostra (dopuszczamy		− m = 0, bo określenie "równanie ma
	4

rozwiązania" zwyczajowo rozumie się jako "ma co najmniej jedno rozwiązanie". Rozwiązania formalne równania (2) istnieją więc dla m spełniających warunek (3); rozwiązania te są określone wzorami:

	1		1
sinx +		= √0,25 − m lub sinx +		= − √0,25 − m, m ≤ 0,25
	2		2

z których wynika, że sinx = − 0,5 + √0,25 − m lub sinx = − 0,5 − √0,25 − m, m ≤ 0,25. Trzeba teraz zadbać, aby liczby po prawych stronach równości "nadawały się na sinx", to znaczy by − 1 ≤ − 0,5 + √0,25 − m ≤ 1 lub − 1 < − 0,5 − √0,25 − m < 1, m ≤ 0,25 − 0,5 ≤ √0,25 − m ≤ 1,5 lub − 0,5 < − √0,25 − m < 1,5, m ≤ 0,25 Pomijając nierówności spełnione w sposób oczywisty dostajemy: √0,25 − m ≤ 1,5 lub − 0,5 < − √0,25 − m, m ≤ 0,25. Dalej już łatwo.

PrzyszlyMakler: Też super sposób, jednak trzeba trochę "być sprytnym"

PW: Od pewnego czasu propaguję ten sposób (będący powtórzeniem rozumowania przy sprowadzaniu funkcji kwadratowej do postaci kanonicznej), bo ma dużo zalet. Nic nie trzeba mówić o wzorach Viéte'a, wierzchołkach paraboli, delcie, żadnych rysunków.

Jack: PW Znajac swoich rowiesnikow − zaden z nich by nie policzyl w ten sposob, ktory oczywiscie jedyne co wymaga to troche umiejetnosci i wiedza ze sinus istnieje w przedziale <−1;1>