Graniastosłup prawidłowy sześciokątny - pole całkowite Tom: Krótsza przekątna graniastosłupa prawidłowego sześciokątnego ma długość 4√3 i jest nachylona do płaszczyzny podstawy pod kątem 30 stopni. Oblicz Pole całkowite.

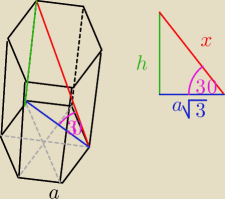
Jack: zalozenia : a,h,x > 0 h − wysokosc graniastoslupa x − krotsza przekatna = 4√3

	1		h
sin 30 =		=
	2		x

x = 2h z pitagorasa x² = 3a² + h² 4h² = 3a² + h² h² = a² h = a zatem x = 2a, h = a wiemy, ze x = 4√3, zatem a = 2√3 = h Pole calkowite = 2*P_p + 6*P_b = gdzie

	a2√3		3a2√3
Pp = 6*		=
	4		2

P_b = a*h = a²

Tom: Czy wynik będzie 18√3 + 8√3 = 26√3 ?

Jack: nie. 3*12√3 + 6*12 = ?

Tom: Dobra już mam, coś źle policzyłem, już chyba ok. Dziękuje za pomoc i poświęcony czas

Tom: Pc = 36√3 + 72 Tak?